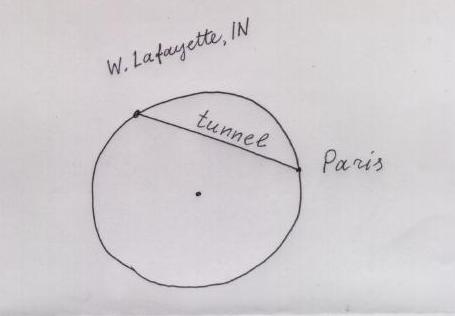
Let us drill a straight tunnel from West Lafayette, IN to Paris, France:

Now let us lay a railroad* in the tunnel. As soon as the brakes of a railroad car in West Lafayette are released, the car will roll down under the force of gravity. It will accelerate, then reach its maximal speed in the middle (=lowest point) of the tunnel, and then decelerate, going up by inertia. If we neglect the energy loss for friction, the Energy Conservation Law will imply that the car will reach Paris just at the same moment when its speed becomes 0. At this moment brakes should be applied, to give passengers time to leave the car, and to take new passengers, going in the opposite direction.
For the whole travel we have not spent a single drop of fuel. All measures should be taken of course to reduce friction as much as possible. I recommend, for example to pump the air off the tunnel. To compensate for the remaining friction between the rail and the wheels, you can use a very small engine.
So the fuel efficiency should be much higher than that of the airlines, or even that of the ships. So the crucial question (crucial for competition with the airlines) is how long will this travel take. This is the question I propose you to investigate. Also please compute the travel time from West Lafayette to Goshen, IN, by a separate tunnel, of course. (We may try to compete with Greyhound too, not only with the airlines). In your computation assume that the density of Earth is constant** everywhere inside. Some relevant information about gravity is in the next section.
**This is unlikely. But this assumption simplifies the problem, and probably is good enough for a rough approximation.
You may find the following two theorems of Newton useful.
THEOREM 1. The gravity force outside of a homogeneous sphere, is the same as if all its mass were in the center.
THEOREM 2. The gravity force inside a homogeneous sphere is zero. (Here is Newton's own proof of Theorem 2).
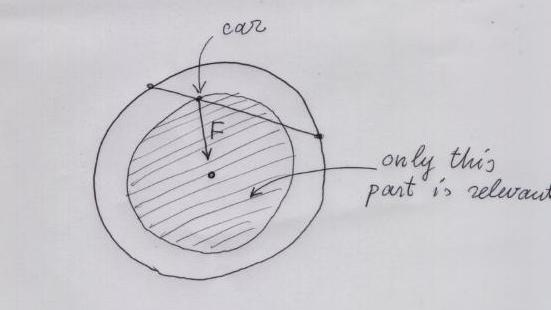
Using these two theorems one can compute the force of gravity at any given point of our tunnel. Look at the picture. Only the part of the Earth which is below the car is relevant. And this part attracts the car to the center of the Earth with the force proportional to the volume of this part.
If after your calculations you will conclude that our Gravity Train is not fast enough, look at an improved version, Brachistochrone Gravity Train, which is the fastest possible of its kind. It is much more mathematically sophisticated than ours, and a tunnel for it requires more digging.
Added on December 7 2013. You can actually see this train going from Australia to England in the movie "Total recall" (2012). Of course the movie makers have all scientific details wrong, even the time of travel:-)