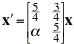
For the given system of equations,
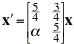
(a) Determine the eigenvalues in terms of 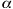 .
.
(b) Find the critical value or values of 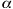 where the qualitiative nature of the phase portrait for the system changes.
where the qualitiative nature of the phase portrait for the system changes.
(c) Draw a phase portrait for a value of 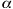 slightly below, and for another value slightly above, each critical value.
slightly below, and for another value slightly above, each critical value.
Using pen and paper, or symbolic manipulation technology, we find
that the eigenvalues of the coefficient matrix in terms of
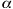 are
are
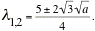
From the equation of the eigenvalues, we see that if 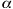 < 0, then the eigenvalues are complex, while if
< 0, then the eigenvalues are complex, while if 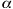 > 0,
then the eigenvalues are real and distinct. Thus, in part (c) below,
we'll look at phase
portraits (generated by dirfield2.m) for
> 0,
then the eigenvalues are real and distinct. Thus, in part (c) below,
we'll look at phase
portraits (generated by dirfield2.m) for
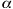 = -0.1 and
= -0.1 and 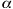 = 0.1.
= 0.1.
If 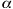 < 0, then the eigenvalues are complex, so we
can expect that the phase portrait will be a spiral. Here is the phase
portrait for
< 0, then the eigenvalues are complex, so we
can expect that the phase portrait will be a spiral. Here is the phase
portrait for 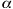 = - 0.1. It is a spiral, but not as tightly
curved as most.
= - 0.1. It is a spiral, but not as tightly
curved as most.
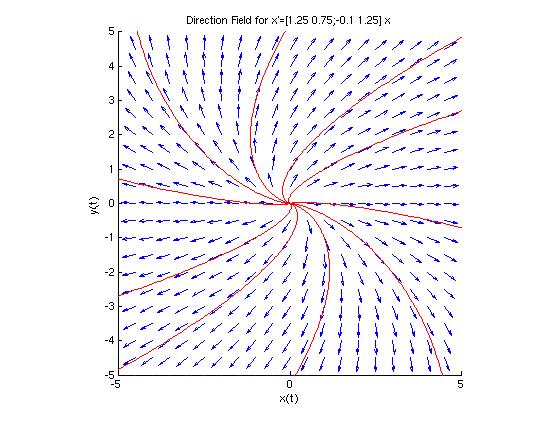
If  > 0, then the eigenvalues are real and distinct,
so the origin is a node. In the graph below, the lines through the
eigenvectors are drawn in black so that we can more clearly see that the
origin is a node.
> 0, then the eigenvalues are real and distinct,
so the origin is a node. In the graph below, the lines through the
eigenvectors are drawn in black so that we can more clearly see that the
origin is a node.

The figure below shows phase portraits for 9 values of
 . In this figure, we can see how as
. In this figure, we can see how as 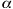 moves from -2 through 0 to +2, the phase portraits change from having the
origin clearly a spiral point to an improper node and then to a node. For
the values of
moves from -2 through 0 to +2, the phase portraits change from having the
origin clearly a spiral point to an improper node and then to a node. For
the values of 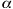 near 0, the phase portraits do not display "classic" behavior: The spirals and nodes are more obscure than for larger magnitudes of
near 0, the phase portraits do not display "classic" behavior: The spirals and nodes are more obscure than for larger magnitudes of 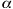 .
.
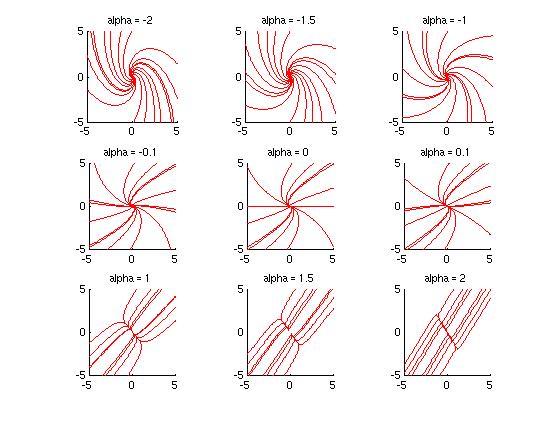
Note: The figure above was generated in MATLAB using the module Ch07Sec06Prob16.m, which was adapted from the code that generates solution curves for the 'dirfield2d' module.