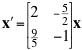
Express the general solution of the given system of equations in terms of real-valued functions. Also draw a direction field, sketch a few of the trajectories, and describe the behavior of the solutions as t approaches infinity.
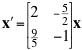
Before we can solve this differential equation, we need to know the eigenvalues and eigenvalues of the matrix
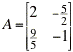
In MATLAB, finding eigenvectors and eigenvalues is done in a single command.
>> A=[2 -5/2;9/5 -1]; % Enter A
>> [V,D]=eig(A)
V = % V is the matrix of eigenvectors
0.7625 0.7625
0.4575 - 0.4575i 0.4575 + 0.4575i
D = % D has the eigenvalues on the diagonal
0.5000 + 1.5000i 0
0 0.5000 - 1.5000i
>>
Thus, the eigenvalues and eigenvectors of A are complex-valued:
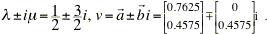
Then, using formula (10) in the text (with n = 2), the general solution of the system of equations is
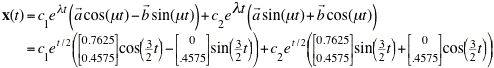
>> dirfield2d
Enter the 2x2 matrix A as [a b;c d] => [2 -5/2;9/5 -1]
Enter the window dimensions for the direction field:
Enter the smallest x value => -5
Enter the largest x value => 5
Enter the smallest y value => -5
Enter the largest y value => 5
Warning: Divide by zero.
> In dirfield2d at 87
Warning: Divide by zero.
> In dirfield2d at 88
Would you like to plot a solution curve on this direction field? (y or n) => n >>
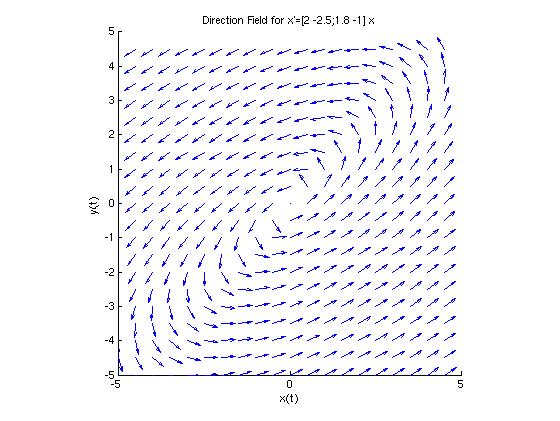
If we had answered 'y' instead of 'n' to the previous question, then 'dirfield2d' will plot as many solution curves as the user requests on top of the existing plot of the direction field. The session to follow plots 5 solutions curves for the initial conditions:
| {(x0, y0)} = | {(1, 1), | (2, 2), | (3, 3), | (4, 4), | (5, 5)} |
Would you like to plot a solution curve on this direction field? (y or n) => y
Enter x(0) for this initial value problem => 1
Enter y(0) for this initial value problem => 1
Would you like to plot another solution curve (y or n) => y
Enter x(0) for this initial value problem => 2
Enter y(0) for this initial value problem => 2
Would you like to plot another solution curve (y or n) => y
Enter x(0) for this initial value problem => 3
Enter y(0) for this initial value problem => 3
Would you like to plot another solution curve (y or n) => y
Enter x(0) for this initial value problem => 4
Enter y(0) for this initial value problem => 4
Would you like to plot another solution curve (y or n) => y
Enter x(0) for this initial value problem => 5
Enter y(0) for this initial value problem => 5
Would you like to plot another solution curve (y or n) => n
>>
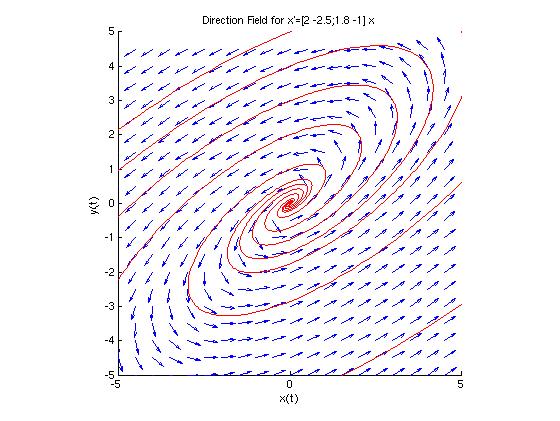
We can see that the origin is a spiral point, and that all non-zero trajectories will spiral out from the origin as t approaches infinity.