Consider the initial value problem
$$5u''+2u'+7u=0,\quad u(0)=2,\quad u'(0)=1$$
(a) Find the solution $u(t)$ of this problem.
(b) Find the smallest $T$ such that $|u(t)|\leq 0.1$ for all $t > T$.
Part (a)
The MATLAB module Ch03Sec03Prob24 will solve a second order linear initial value problem and plot the solution in the case of constant coefficients and complex roots of the characteristic equation. The differential equation is entered as a vector that contains the coefficients of the characteristic equation (enclosed in square brackets). The program also prompts the user for the domain of the function for the purpose of producing a graph. Here is a transcript of the MATLAB session that produced the graph below:
>> Ch03Sec03Prob24
Enter the characteristic polynomial as a vector [a b c] => [5 2 7]
We will solve the homogeneous equation:
5 u'' + 2 u' + 7 u = 0.
Enter the initial value of u => 2
Enter the inital value of u' => 1
Enter the domain of the function:
Minimum t-value => 0
Maximum t-value => 20
The solution to the IVP is u(t) = 2*exp(-0.2*t).*cos(1.16619*t) + 1.20049*exp(-0.2*t).*sin(1.16619*t).
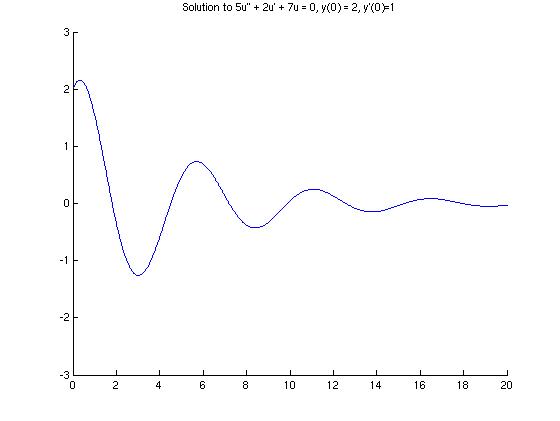
Part (b)
From the graph in part (a), we can see that the graph is oscillating, but approaches zero. It seems that for t around 15, the function values are between $-0.1$ and $0.1$, but this is a really rough guess. Let's use MATLAB to get a better approximation of $t$ so that $|u(t)|<0.1$. The data points are stored in arrays titled 'tpts' and 'upts'.
>> size(upts) % Remind ourselves that there are 1000 data points
ans =
1 1000
>> for i=1:1000
j=1001-i; % Look backwards through data points
if (abs(upts(j)) > 0.1) % Quit looking when |u| > 0.1 and then exit loop
disp(sprintf('=> When t = %.5g, u = %.5g is less than 0.1 in absolute value.', tpts(j+1),upts(j+1)))
return
end % End if statement
end % End for loop
=> When t = 14.515, u = -0.099663 is less than 0.1 in absolute value.
Thus, for all $t> 14.515$, we have $-0.1< u(t)<0.1$.