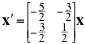
Find the solution of the given initial value problem. Draw the trajectory of the solution in the x1x2-plane and also draw the graph of x1 versus t.
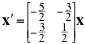
We can use MATLAB to do the individual calculations, but we need to find the generalized eigenvector 'eta' step-by-step.
>> A = [-5/2 3/2;-3/2 1/2]; x0=[3;2]; % Define A and initial condition vector x0
>> [V,D]=eig(A)
V =
0.7071 -0.7071
0.7071 -0.7071
D =
-1.0000 0
0 -1.0000
>> L=D(1,1); % L is the repeated eigenvalue.
>> v=[V(1,1);V(2,1)]; % v is the repeated eigenvector.
>> % 'eye(2)' is the 2x2 identity matrix.
>> B=rref([A-L*eye(2) v]) % Solve this system manually to find eta.
B =
1.0000 -1.0000 -0.4714
0 0 0
>> eta=[B(1,3);0]; % Found by inspection of B.
>> % Solution is X(t)=c1*exp(Lt)*v + c2*exp(Lt)*(tv + eta)
>> coeffs=[v eta]\x0;
>> c1=coeffs(1); c2=coeffs(2);
>> % We now know all pieces of X(t). Use '.*' for multiplication.
>> strx1=sprintf('%g*exp(%g*t)*%g + %g*exp(%g*t).*(t*%g+%g)', c1,L,v(1),c2,L,v(1),eta(1));
>> strx2=sprintf('%g*exp(%g*t)*%g + %g*exp(%g*t).*(t*%g+%g)', c1,L,v(2),c2,L,v(2),eta(2));
>> % Convert from strings to functions.
>> x1 = inline(strx1,'t'); x2 = inline(strx2,'t');
>> disp(x1) % Here are the solutions.
Inline function:
x1(t) = 2.82843*exp(-1*t)*0.707107 + -2.12132*exp(-1*t)*(t*0.707107+-0.471405)
>> disp(x2)
Inline function:
x2(t) = 2.82843*exp(-1*t)*0.707107 + -2.12132*exp(-1*t)*(t*0.707107+0)
>>
Now we know that the component functions of the solution are
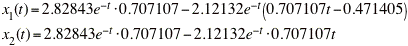
Let's look at a parametric plot of the trajectory in the x1x2-plane:
>> tpts=-10:0.01:10; % Define t-values
>> figure; hold on;
>> plot(x1(tpts),x2(tpts)); % Plot parametrically.
>> xlabel('x_{1}(t)'); ylabel('x_{2}(t)');
>> title('x_{2}(t) -vs- x_{1}(t)');
>> axis([-.5 2 -.5 2]); % Resize window to show details.
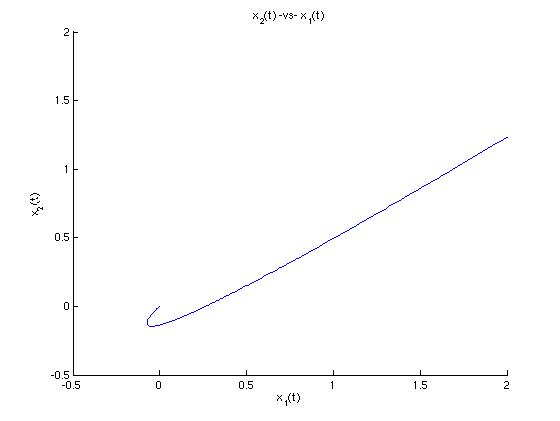
We see deduce that this trajectory is moving toward the origin because the exponential functions are decaying. Let's look now at a graph of x1 -vs- t and see how the two graphs relate.
>> figure; hold on;
>> plot(tpts,x1(tpts)); % Plot x1(t) -vs- t
>> xlabel('t'); ylabel('x_{1}(t)'); title('x_{1}(t) -vs- t');
>> axis([0 10 -.5 2]); % Resize window to see details.
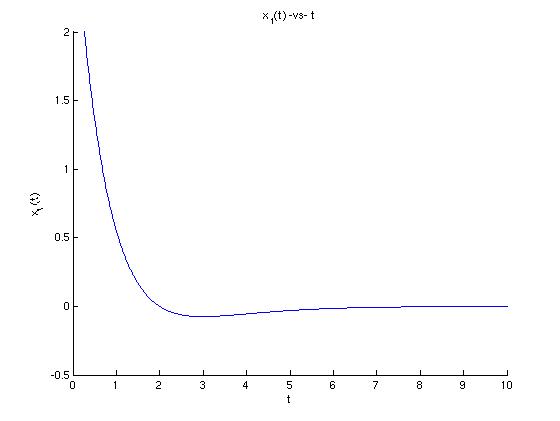
We can estimate the the bottom of the "hook" in the graph of solution curve occurs around t = 3 from looking at the minimum point of the graph of x1. So, as we can see from reading both graphs together, x1 decreases rapidly as t goes from negative infinity to about 3, then x1 increases again (but quite slowly) to 0 as t goes from about 3 to positive inifinity. We can intuit the direction of motion from either graph, but only the graph of x1 -vs- t gives us a sense of how quickly the motion occurs.