David Jerison (Cambridge)
Existence and regularity for two-phase free boundary problems
Abstract: We will discuss joint work with L. A. Caffarelli and
C. E. Kenig on existence and regularity of elliptic free boundary problems.
These problems are motivated by the example of the Prandtl-Batchelor problem
in two variables. The novelty is that the inhomogeneous term can be discontinuous
across the free boundary.
Lavi Karp (Haifa)
A free boundary problem and Newtonian potential
Abstract: Suppose  is a bounded domain in
is a bounded domain in 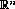 with real analytic boundary
with real analytic boundary 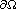 , and suppose
f is a real analytic function in a neighborhood of
, and suppose
f is a real analytic function in a neighborhood of  . Then, as a consequence of Cauchy Kovalewskii's theorem, the Newtonian
potential of the density f over
. Then, as a consequence of Cauchy Kovalewskii's theorem, the Newtonian
potential of the density f over  (which is harmonic out of
(which is harmonic out of  ), has a harmonic continuation into
), has a harmonic continuation into  .
.
We are considering the inverse problem, that is, suppose the Newtonian
potential of f has a harmonic continuation into  , does it implies that
, does it implies that 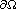 is real analytic. We shall see that the answer to that question rely upon
the investigation of global solutions:
is real analytic. We shall see that the answer to that question rely upon
the investigation of global solutions:
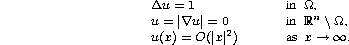
We will also discuss the classification of global solutions and its
relation to Newton's theorem which asserts that homeoidal ellipsoid induces
no gravity force in the cavity. This talk based on a joint work with L.
Caffarelli and H. Shahgholian.
Bernd Kawohl (Köln)
Isoperimetric inequalities for plate eigenvalues
Abstract: The well-known Faber-Krahn inequality states that among
all clamped membranes of given area the circular one has minimal fundamental
frequency. In my lecture I shall recall different methods of proof for
it and report on related results for plate eigenvalues. These lead to new
questions on the regularity of sets which minimize eigenvalues.
Claudia Lederman (Buenos Aires)
Uniqueness and agreement of solution in a two phase free
boundary problem from combustion
Abstract: We consider the following two phase free boundary problem:
find a function u(x,t), defined in 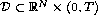 , satisfying that
, satisfying that
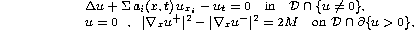
(M>0 constant). In addition, Dirichlet or Neumann
data are specified on the parabolic boundary of 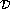 .
.
This problem arises in combustion theory as a limit situation in the
propagation of premixed flames (high activation energy limit).
The problem admits classical solutions only for good data and for small
times. Different generalized concepts of solution have been proposed, among
them the concepts of limit solution and viscosity solution. In the work
we present here we find conditions under which the concepts of classical,
limit and viscosity solution agree and produce a unique solution. This
is a joint work with J.L. Vazquez and N. Wolanski.
Peter A. Markowich (Vienna)
Singular limits of mean field equations
Abstract: Mean field equations describe thermal equilibrium states
of interacting species of particles in plasmas. Typically, these equations
take the form of a semilinear elliptic equation with a nonlocal L1-nonlinearity.
We show that mean field equations arise as large time limits of (singular)
diffusion equations with Poisson coupling. The main tool in this proof
are generalized Sobolev inequalities and the main difficulty in the proof
lies in the limited regularity due to the occurance of free boundaries
in the porous medium case. Also, the singular perturbation limit is analysed
- leading, in certain parameter regimes, to a double obstacle problem.
Here, the free boundaries are of particular physical importance since they
separate vacuum from non-vacuum regions. The singular perturbation analysis
is based on the dual variational formulation with a functional which is
not necessarily coercive (in the fast diffusion case).Particular emphasis
is given to the convergence (and geometry) of the free boundary in the
singular perturbation limit (porous medium case). The talk is based on
a joint papers with L. Caffarelli, J. Dolbeault, C. Schmeiser and A. Unterreiter.
Jorge Salazar (Lisbon)
Regularity of viscosity solutions of fully nonlinear elliptic equations
with free boundaries
Abstract: We study some properties of viscosity solutions of
fully nonlinear elliptic equations of the form
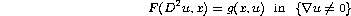
where the solution u is continuous. 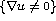 is interpreted as a condition on the test functions, which is a very weak
condition.
is interpreted as a condition on the test functions, which is a very weak
condition.
We establish existence of solutions under some restrictions on F.
As a first step in the study of regularity, we eliminate the condition
on the gradient by showing that the solutions verify two elliptic inequalities.
This result allows us to apply the powerful machinery of the nonlinear
elliptic theory and obtain the Alexandroff-Bakelman-Pucci estimate, Harnack's
inequality and 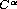 regularity. We also discuss
regularity. We also discuss 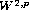 regularity, using the notion of
regularity, using the notion of 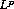 -viscosity solutions. In the case of equation
-viscosity solutions. In the case of equation 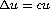 on
on 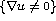 , where c is a positive constant, we prove that u is
, where c is a positive constant, we prove that u is 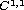 .
.
When the right hand side g of the equation is strictly positive,
we prove that the (n-1)-dimensional Hausdorff measure of the free
boundary is finite. As an application, we study the equation 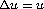 on
on 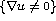 , on a bounded, convex, plane domain
, on a bounded, convex, plane domain  , such that
, such that  on
on 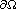 . We prove that there is at most one connected component of
. We prove that there is at most one connected component of 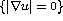 with non empty interior. Besides, such a component is
convex.
with non empty interior. Besides, such a component is
convex.
Sandro Salsa (Milan)
A class of free boundary problems with application to the theory of
conductivity
Abstract: We describe some recent results obtained in a joint
work with Athanasopoulos and Caffarelli concerning a class of free boundary
problems and their application to the uniqueness in a classical inverse
problem of conductivity. The regularity of the free boundary in analyzed
in details under minimal conditions.
Nina Ural'tseva (St. Petersburg)
How the free boundary can meet the prescribed one
Abstract: The behaviour of free boundaries near the prescribed
ones is studied for some classes of free boundary problems. In the case
of zero obstacle problem it is proved that the free boundary touches tangentially
the given boundary provided the latter is smooth and the boundary values
of the solution vanish in a neighbourhood of a contact point. For more
general free boundary problem, without sign restrictions on a solution,
the same behaviour of the free boundary near contact points is established
under certain conditions.
Georg S. Weiss (Tokyo)
The free boundary of a thermal wave in a strongly absorbing medium
Abstract: In dimension 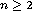 we obtain regularity of the free boundary
we obtain regularity of the free boundary 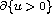 of non-negative solutions of the heat equation with strong absorption
of non-negative solutions of the heat equation with strong absorption
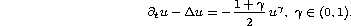
Our approach is motivated by methods in Liapunov's stability theory
and by results concerning the Plateau problem. We use an epiperimetric
inequality in order to obtain a decay estimate for the energy
associated with the equation. By a monotonicity formula this leads to homogeneity
improvement and to unique tangent cones. The regularity of the free
boundary follows then from topological arguments.