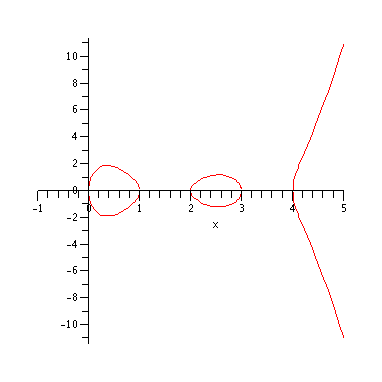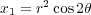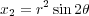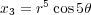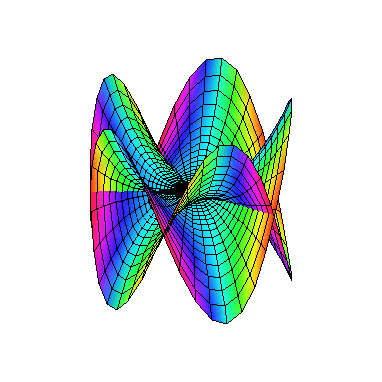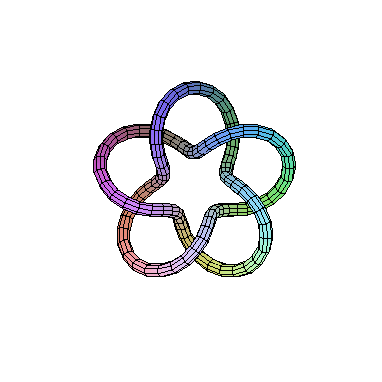A hyperelliptic curve is defined by an equation y2 = p(x) where p(x) is a
polynomial of degree at least 5 with distinct roots.
The last condition guarantees it's nonsingular.
General theory tells us that this
would have large genus (i.e. many holes).
For example,
 should be a genus two surface or "two-holed doughnut".
should be a genus two surface or "two-holed doughnut".
 This is partly evident from the real graph:
This is partly evident from the real graph:
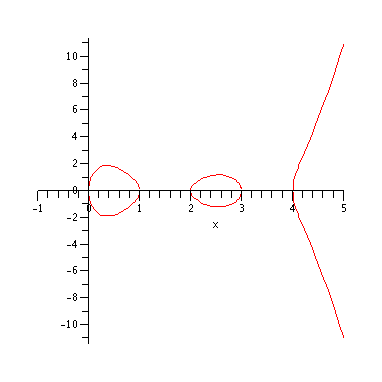 where the holes can be thought of as the gaps between the components.
where the holes can be thought of as the gaps between the components.
We were able to parameterize an elliptic curve by using elliptic
functions on the complex plane. These were periodic with respect to
a tiling of the plane by parallelograms. For hyperelliptic curves,
we replace the plane by the disk, and tile these by polygons which
are regular in the sense of hyperbolic geometry (in which the "straight
lines" are circles meeting the boundary circle at right angles).
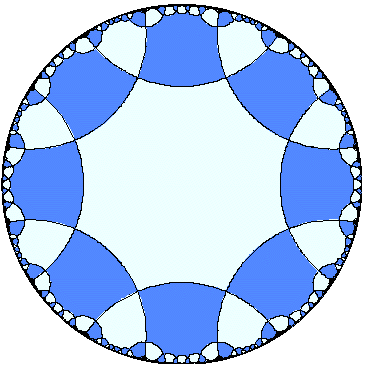 We can then parameterize such curves by using functions which are almost periodic or automorphic
with respect to this tiling. This is usually formulated in terms of
the group of symmetries of the tiling, rather than the tiling itself.
Some discussion of these matters can be found for example in Siegel,
Topics in complex function theory vol 2.
We can then parameterize such curves by using functions which are almost periodic or automorphic
with respect to this tiling. This is usually formulated in terms of
the group of symmetries of the tiling, rather than the tiling itself.
Some discussion of these matters can be found for example in Siegel,
Topics in complex function theory vol 2.
Making this explicit enough to draw a graph would be a daunting
task. So we look at the simpler case where all the roots of p(x)
come together. Namely, y2 = x5. This
is a singular curve called a cusp. It is easy to see that x = t2, y = t5 gives a rational parameterization. This
can arrived at by carrying out a resolution proceedure as above, but
this time with two blow ups. Switching
to polar coordinates (for purely aesthetic reasons) and taking real and imaginary parts as above, leads
to
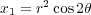
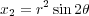
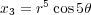 This yields
This yields
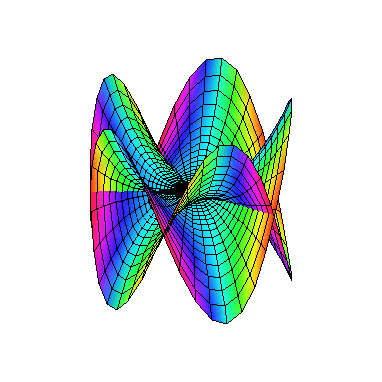 Now take a look at the outer edge of this picture. The way it is
drawn, it repeatedly crosses itself. But we know this really
represents a defect of our depiction more than anything else.
To get a better feeling for what this ought to look like, form
the intersection of our cusp with a small
sphere
∣x∣2 + ∣y∣2 = ε 2.
This is called the link of the singularity. The sphere can
be identified with R3 plus a point at infinity,
and the link is a knot in this space. In this case, the link
is a so called (2,5)-torus knot which looks as follows
Now take a look at the outer edge of this picture. The way it is
drawn, it repeatedly crosses itself. But we know this really
represents a defect of our depiction more than anything else.
To get a better feeling for what this ought to look like, form
the intersection of our cusp with a small
sphere
∣x∣2 + ∣y∣2 = ε 2.
This is called the link of the singularity. The sphere can
be identified with R3 plus a point at infinity,
and the link is a knot in this space. In this case, the link
is a so called (2,5)-torus knot which looks as follows
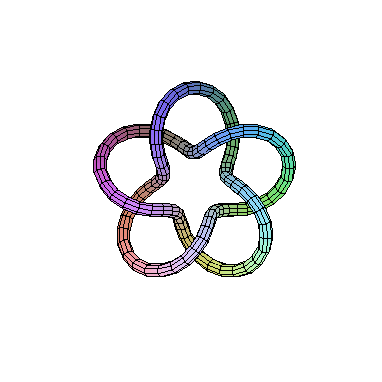 If we did this for a nonsingular point, we would have gotten an
unknotted circle. So the amount of "knottedness" is really telling us how bad
the singularity is.
If we did this for a nonsingular point, we would have gotten an
unknotted circle. So the amount of "knottedness" is really telling us how bad
the singularity is.
Return to first page.