Sato-Tate
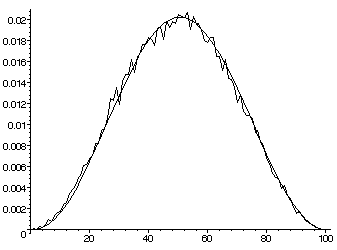
Given an elliptic (or higher genus) curve over Q, the
(generalized) Sato-Tate conjecture predicts how the number of points
N(p) over its reduction mod p varies with p. For an elliptic curve without
complex multiplication, the conjecture predicts that the angles
arccos[(1+p-N(p))/2sqrt(p)] obey the sin^2 law. Here is
a plot of the theoretical versus actual distributions for
all (good) primes less than 500,000 for y^2=x(x-1)(x-3),
( the horizontal axis is scaled so that 100 corresponds to Pi).
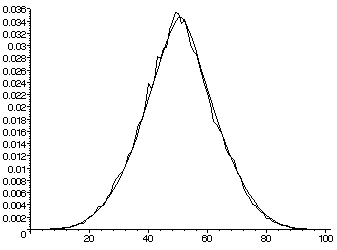
Assuming the generalized Sato-Tate, a similar prediction
can be made for the distribution of the numbers
(1+p-N(p))/2sqrt(p) for a curve of genus 2 with "big monodromy".
Below is a plot (scaled appropriately)
for the theoretical versus actual distributions of these numbers
for all good primes less than 500,000 for y^2=x(x-1)(x-2)(x-3)(x-7).
Further details can be found in
my notes based on
a talk at U. of Arizona.
These graphs were generated using Maple, however the raw
number crunching was handled by some C programs
which ran for several hours on my Apple G4/450 runinng linuxppc.
The C source code for this is available
here (you'll need to "untar" this
and read the instructions).
A more serious computation has been carried out by Vikram Buddhi.
Here is plot of the predicted probability distribution
of the pair of "Frobenius angles" (suitably scaled)
for the above genus 2 curve
versus the actual one after 500 hours of computation on one of Suns
(using a brute force method).
Many more extensive calculations have been carried out by Bill Butske,
[PhD Thesis, Purdue, 2005].