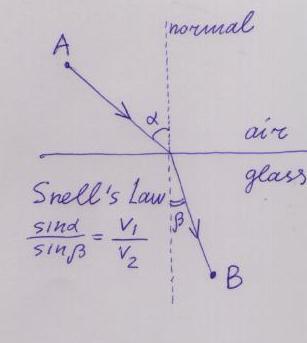
When you look at a straw in a cup of tea or water (don't put ice to your cup for this experiment!) it looks bent at the place where it crosses the water surface. The reason is that light rays do not follow a straight line when they cross a boundary of two different media (like air and water, or air and glass). This phenomenon, called refraction, is well known to anybody who ever looked at underwater objects through the surface of water. (It is even more interesting to look at objects in the air from under water).
Apparently the precise law of refraction was not known to the ancients, and the glory of this discovery belongs to a Dutch astronomer Willebrod Snell, or Snellius, (1621). The law says that:
`The incident ray, the refracted ray and the normal to the surface lie in the same plane; the ratio of sines of the incidence angle and the refraction angle is constant, depending only of the media separated by the surface. (The incidence angle and the refraction angle are the angles formed by corresponding rays with the normal to the surface).

It was Pierre Fermat, who found an following interpretation of this law, similar to the interpretation of the law of reflection law by Hero of Alexandria.
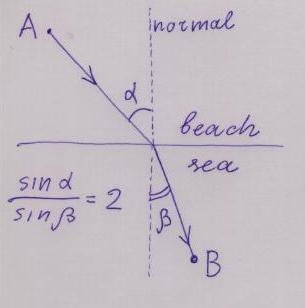
Imagine a straight seashore, separating the sea from a beach. A lifeguard sitting at a point A on the beach spots a person drowning at a point B in the sea. Given that the lifeguard can run on the beach 3 times faster than she can swim, what way should she choose from A to B to reach B in shortest time?
For modern undergraduates, especially those taking differential equation courses, this should be an easy calculus exercise, especially if they know the answer in advance: The shortest time path is the broken line going straight from A to a point M on the shore, then straight to B. `The incidence angle', that is the angle between AM and the normal to the shore, and the `refraction angle', the one between BM and the normal to the shore have the property that the ratio of their sines is 2. In general the ratio of sines should be equal to the ratio of speeds in the corresponding media.
(Fermat died in 1665, the same year when Newton apparently `discovered calculus', but Fermat knew how to differentiate, to find maxima and minima, and to find volumes by integration).
It follows from this result of Fermat, that light chooses the path which will take shortest time to go! In Fermat's time it was really hard to measure the speed of light to verify his theory. Because, as you know, this speed is enormous, more than 180,000 miles per second. The very fact that this speed is finite was discovered by Olaus Roemer 10 years after Fermat's death. (Can you guess how he did it, or propose some other way, available in XVII century? Roemer measured it with about 15% error. I think only in XIX century it was possible to measure the speed of light in a media, other than vacuum. The measurements show, of course that Fermat's bold guess was correct.) Another difficulty was of `philosophical' nature: if light is a jet of some particles, how do these particles know, which way takes the least time?
Sources:
Sir E. Whittaker, A history of the theories of aether and electricity,
vol. 1: The classical theories, third edition, Harper, NY, 1960.
Feynman Lectures on Physics, vol. 1 and vol. 2, ch 19.