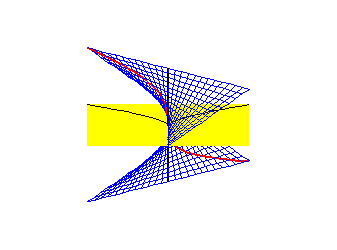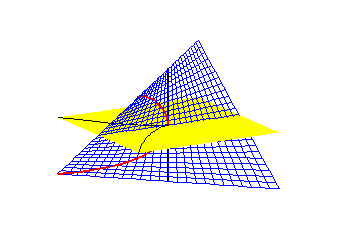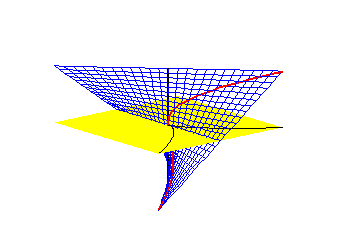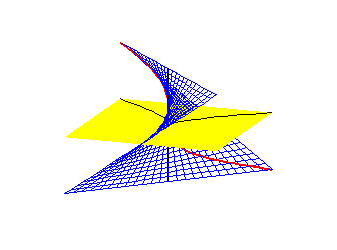

In order to get a feeling for what algebraic geometry is, let's to go through some examples. Consider the space of 2x2 matrices over a field k with trace 0. This consists of matrices of the form which can be identified with points (x,y,z) of three dimensional affine space . In these coordinates the determinant . The determinant is an algebraic map, and the fibers
Let's study the geometry of these sets. Suppose k=C, then I claim that is isomorphic to whenever t is nonzero. To see this, choose a such that , then the map defines an isomorphism between and ; this can be checked by comparing coordinate rings. ( This works even if C is replaced by an algebraically closed field. But it fails in general. For example when k =R, is connected in it's usual topology while isn't.) I claim that is a homogeneous space which implies that any point looks like any other point. To see this, observe that the algebraic group acts on by matrix conjugation, and that this is a transitive action.
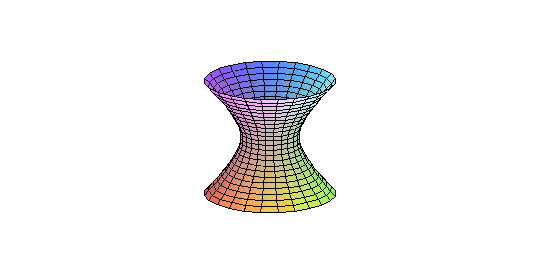
is the space 2x2 matrices with zero trace and zero determinant. It follows by the Cayley-Hamilton theorem that this is precisely the set of nilpotent matrices. The zero matrix is a singular point of this set, while the other points are nonsingular. It follows that is not homogenous, and therefore is not isomorphic to . Alternatively, these cannot be isomorphic since all the points of are nonsingular.
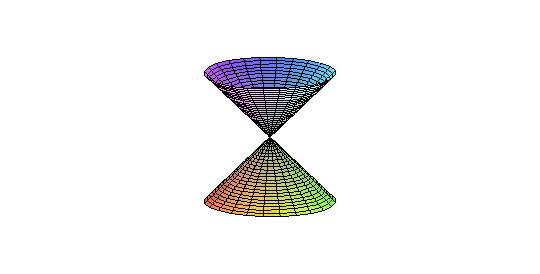
What we've been doing so far is affine geometry. We get a little more insight into the structure of these sets by doing projective geometry. A matrix in has 1 and -1 as its eigenvalues. The eigenvectors span two distinct lines in . Conversely, a pair of distinct lines determines an element of . Thus we have a bijection, and in fact isomorphism, between the and the product of two copies of the projective line minus the diagonal. Thus is a so called doubly ruled surface. These rulings, which are fibers of the projections onto the factors, are embedded as lines in . In fact, after a linear change of coordinates the embedding of into extends to the Segre embedding of to .

It follows from above that is birational to the and therefore to . However, it is not isomorphic to . This is because the coordinate ring is a unique factorization domain, while isn't (the image of yz can be factored in two different ways).
The second example, which is the one indicated in the picture at the top, is the blow up of the affine plane. This consistis of a quasiprojective variety Bl and a morphism , where Bl consists of pairs (x,L) where x is point in and L point in containing x, and p(x,L) = x. The morphism p induces isomorphism . Therefore p is a birational equivalence. However, p is not an isomorphism, since the preimage is rather than a point. Bl can be described as a union of two affine varieties, and glued via . is blue surface depicted above.
The curve in is singular at (0,0). Its preimage under p, called its total transform, is the union of E with a curve (the red curve). , which can be described as the closure of the preimage of C-{(0,0)}, is called the strict transform. This curve lies in and is given parametrically by , . The map given by is an isomorphism, since is the inverse, therefore is smooth. Since and C are isomorphic away from (0,0), they are birational. The map on coordinate rings is given by , , so A(C) can be identified with the subring of k[s] generated by and . is an example of resolution of singularities.
Harris is the text for this class (although I won't follow it too closely).
This and additional references arewith(plots): Bl := plot3d([x,x*t, t], x=-1..1, t=-1..1, style=WIREFRAME, color =blue):A2 := plot3d([x,y,0], x=-1..1, y=-1..1, color=yellow, style=PATCHNOGRID):
E := spacecurve([0,0,t], t=-1..1, color=black, thickness=2):
C := spacecurve([s^2, s^3, 0], s=-1..1, color=black, thickness=1):
C2 := spacecurve([s^2,s^3,s], s=-1..1, color=red, thickness=2): display({Bl,A2, E, C, C2});
For doing calculations in algebraic geometry and commutative algebra, Grayson and Stillman's Macaulay2 program is more powerful than Maple or Mathematica. Documentation is available on the web or as a (very big) pdf file. To get a sense for what it can do, let's consider some simple examples. Start the program by typing M2 in a terminal window of one of our Suns or whatever machine you're using. (If you plan to do anything serious, you'll need to learn how to run it under emacs.)
If this doesn't work then read this.1. As a first example, let's check a special case of the Cayley-Hamilton theorem. At the prompt (i1:) type
R = QQ[x_1..x_4]This sets up a polynomial ring over Q (= QQ in Macaulay) in 4 variables. Next define the ideal I generated by det and trace of the "universal" 4x4 matrix M by typing
M = matrix{{x_1,x_2},{x_3,x_4}}The algebraic set V(I) in (= space of 2x2 matrices) is the set of matrices with det= trace = 0 Let Nilp be the set of matrices whose square vanishes. The entries of generate an ideal J which can be constructed byD = det M
T = trace M
I = ideal {D, T}
J = ideal M^2Then Nilp = V(J). By the Cayley-Hamilton theorem, V(I) coincides with Nilp as well. Let's check this directly. In order verify V(I) = V(J) (over any algebraically closed field of char. 0), it's enough, by the Nullstellensatz, to check the equality of the radicals of I and J:
radical I == radical JExercise: check whether I = J? If not, then what goes wrong?
2. Next, let's check that the hypersurface in has exactly one singular point at (1,1,0) over an algebraically closed field of large positive characteristic (Macaulay2 computes more efficiently over finite fields).
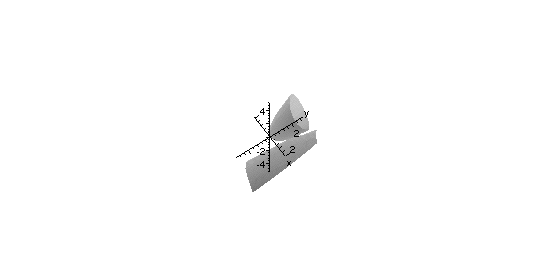
erase symbol xThe graph (which is a bit misleading) suggests that the hypersurface might be reducible. We can check that it's irreducible over the prime field Z/31991 by trying to factor it:R = ZZ/31991[x,y,z]
f = z^2 -(y-1)*(y^2-x)
factor fNext define the ideal Jac generated by f and its partials.
Jac = ideal { f, diff(x,f), diff(y,f), diff(z,f)}The singular locus of f is precisely V(Jac). It is enough by the Nullstellensatz to check the radical of Jac is the maximal ideal (x-1,y-1,z)
radical Jac
3. For the last example, let's identify with space of 2x4 matrices. Consider the morphism given by sending a matrix to the vector of its 2x2 minors (in some order). Let X be the image of F, and let's find I(X). (In more geometric terms, we're determining the Pluecker equations for the Grassmanian of 2-planes in affine 4-space.) Let R and S be the coordinate rings of these affine spaces.
erase symbol xLet p be homomorphism from S -> R determined by P.erase symbol y
R = QQ[x_1..x_8]
S = QQ[y_1..y_6]
M = genericMatrix(R,x_1,2,4)Then I(X) = ker(p)M2 = exteriorPower(2,M)
p = map(R,S, M2)
ker pWhen we're finished, type
quitBack to beginning.
This information is relevant for people usings Suns at Purdue Math only:
If "M2" doesn't work, it means that the command is not on your path. You'll need to add it. Unfortunately, there are two different locations in our dept. depending on the version of the operation system.
Typeuname -rIf it's 5.5.1, use /opt/Macaulay2-0.8.60/bin If it's 5.8, use /pkgs/macaulay2-8.60/bin/ If all else fails, you can use my personal version /.amd_mnt/banach//export/u7/dvb/Macaulay2/bin on a Solaris 5.8 machine.
Mathematics may be timeless, but this information certainly isn't. If things don't work in the future, check here again. (Note: I'm currently, as of fall '02, running linux on my office machine, so I probably won't bother updating the Sun stuff.)
This web page was created on a Mac running yellowdog linux and MacOS9, with amaya, emacs, itex2html, mozilla, Macaulay2, Maple, GifBuilder (the latter two running under MacOS). The equipment was purchased through an NSF grant.
Last revision 11/08/02