In this final section, we tie up some loose ends and give some hints about how to study these objects more rigorously. We assume a bit more mathematical sophistication now, and explain some of the algebraic aspects of the subject that we have neglected so far.

First, we want to clarify the phrase “points at infinity” which has been used frequently without being precisely defined. This is partly a matter convention. The key requirement is that after adding points, we get a compact space, although there are other condsiderations which certain choices better than others. In real analysis, it is convenient to have two points ±∞, whereas in complex analysis it better to have just one. For the plane C², it is again necessary to have several points, but this time infinitely many. The simplest scheme comes by passing to the projective plane CP², where we add one point at infinity for each family of parallel lines in C². Equivalently these points correspond to lines through 0. For any curve X ⊂ C², we can take it closure in CP² to get a so called projective algebraic curve. In other words, we attach a point at infinity if it corresponds to something like an asymptote. If X is defined by a degree d polynomial

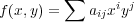
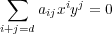
Given a curve X as above, with f irreducible, the basic invariant is the field C(X) of meromorphic functions on X (these are required to be meromorphic at points of infinity also). This is called the function field of X For the line, C(X) is equal to a field of rational functions. For an elliptic curve, this is the associated field of elliptic functions. It has an algebraic description given as follows. The coordinate ring O(X) is the ring of functions which are restrictions of polynomials from C². In more algebraic terms, this can be defined as the quotient ring of C[x,y] by the ideal (f(x,y)) generated by f. Since f is irreducible, the ideal is prime, and so it follows O(X) is an integral domain.

Theorem. C(X) is nothing but the field of fractions of O(X). In particular, it is a field of transcendence degree 1 over C, which means that it is an algebraic extension of a field of rational functions in one variable. Conversely, any such field is the function field of a plane curve.

Two different plane curves may give rise to the same field. However, there is a uniqueness if we impose nonsingularity everywhere. We can now state one of the main results of the subject:

Theorem. There is a one to one correspondence between isomorphism classes of fields of transcendence degree 1 over C and isomorphism classes of nonsingular projective algebraic curves (not necessarily in the plane).

Although we won’t attempt to prove this, it is worth understanding how to recover the set of points from the field. A discrete valuation on a field K is a surjective map v : K -{0}→ Z satisfying

1. v(fg) = v(f) + v(g)
2. v(f + g) ≥ min(v(f),v(g))

For example, given a C, for any polynomial, define v_a(f(x)) = n if (x - a)ⁿ is the highest power of (x - a) dividing f(x). Then v_a(f(x)∕g(x)) = v_a(f) - v_a(g) gives a discrete valuation on the field C(x) of rational functions. There is one more valuation given by v_∞((f(x)∕g(x)) = -v₀(f(x)∕g(x)). In general, given a nonsingular projective algebraic curve X, its points are in one to one correspondence with the set of discrete valuations points on C(X).

Return to first page.