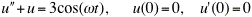 .
.Consider the forced but undamped system described by the initial value problem
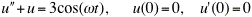 .
.
(a) Find the solution u(t) for 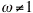
(b) Plot the solution u(t) versus t for 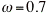 ,
,
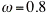 , and
, and 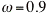 .
Describe how the response u(t) changes as
.
Describe how the response u(t) changes as 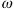 varies in this
interval. What happens as
varies in this
interval. What happens as 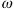 takes on values closer and
closer to 1? Note that the natural frequency of the unforced system is
takes on values closer and
closer to 1? Note that the natural frequency of the unforced system is
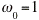 .
.
The solution to this initial value problem for
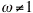 must be found by hand or by using technology
with symbolic
manipulation capabilities. Here is the solution:
must be found by hand or by using technology
with symbolic
manipulation capabilities. Here is the solution:
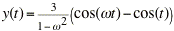
The MATLAB module Ch03Sec09Prob18.m plots
one solution to this initial value problem for a value of
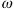 specified by the user.
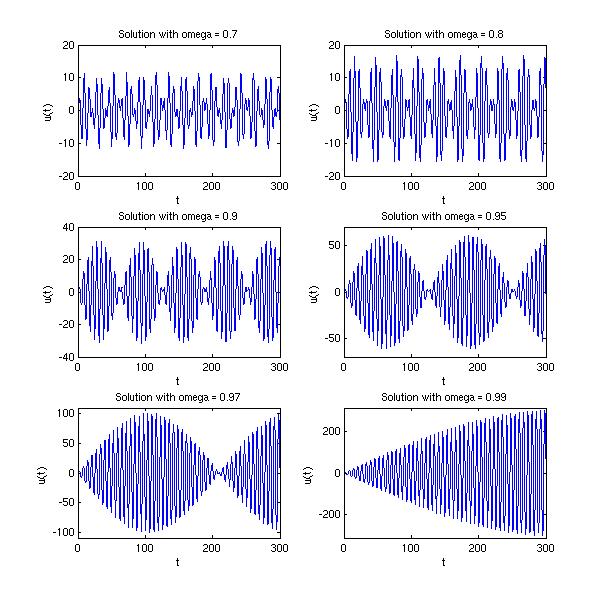
For brevity, six of these plots are shown together below, created by the following MATLAB code.
specified by the user.
For brevity, six of these plots are shown together below, created by the following MATLAB code.
>> tmin=0;
>> tmax=300;
>> figure
>> hold on
>> omega=[.7 .8 .9 .95 .97 .99]; % we'll plot one solution for each of these values
>> for i=1:6 % Loop -- repeat once for each omega
ustr=sprintf('3/(1-%g^2)*(cos(%g*t)-cos(t))',omega(i),omega(i));
u=inline(ustr,'t');
subplot(3,2,i) % selects plot i of a 3x2 grid of plots
fplot(u,[0,tmax]) % plot solution curve
amp=abs(6/(1-omega(i)^2)); % determine height of plot based on
ymax=10*(ceil(amp/10)); % amplitude of graph
axis([tmin tmax -ymax ymax]);
xlabel('t') % label axes and plot
ylabel('u(t)')
title(sprintf('Solution with omega = %g',omega(i)));
end
>>
 .
.
Notice that in all six of these graphs, the horizontal scale is the same,
although the vertical scale changes from figure to figure. We can see from
this set of graphs that
as 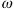 approaches 1, the period of the envelope function
(what we see as 'pulses') increases. The amplitude of the envelope function
increases
as well.
approaches 1, the period of the envelope function
(what we see as 'pulses') increases. The amplitude of the envelope function
increases
as well.
(Note: In the last figure, the graph does have 'pulses', the period is just longer than the 300 units allowed by the graphing window.)
Further questions to explore:
What happens if 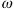 = 1? What happens for values of
= 1? What happens for values of 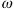 greater than 1?
greater than 1?