Lesson 35 (7.6)

7.6 Complex Eigenvalues

Consider the system of differential equations:

$$\vec{x}'=A\vec{x}$$

where $A$ has **complex eigenvalues**.

Example 1

For example, consider the system:

$$\vec{x}'=\begin{pmatrix}0&-1\\ 1&0\end{pmatrix}\vec{x}$$

The characteristic equation is found by calculating the determinant of $(A - \lambda I)$:

$$\begin{vmatrix}-\lambda&-1\\ 1&-\lambda\end{vmatrix}=\lambda^{2}+1=0$$

This yields the eigenvalues $\lambda = \pm i$.

Observing the **direction field** gives clues about the solution:

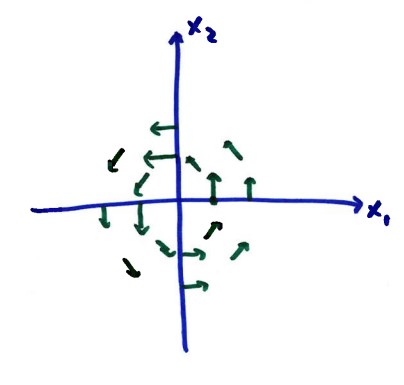
Direction field showing the vectors point in counterclockwise rotation

For $\vec{x}=\begin{pmatrix}1\\ 0\end{pmatrix}$, $\vec{x}'=\begin{pmatrix}0&-1\\ 1&0\end{pmatrix}\begin{pmatrix}1\\ 0\end{pmatrix}=\begin{pmatrix}0\\ 1\end{pmatrix}$.

For $\vec{x}=\begin{pmatrix}0\\ 1\end{pmatrix}$, $\vec{x}'=\begin{pmatrix}0&-1\\ 1&0\end{pmatrix}\begin{pmatrix}0\\ 1\end{pmatrix}=\begin{pmatrix}-1\\ 0\end{pmatrix}$.

The direction field shows that the solutions are **circles (ovals)**.

Each component of the solution is **periodic**.
This suggests the solutions involve **sines and cosines**.

Solving for Eigenvectors

The form of a complex solution is $\vec{x}(t) = e^{\lambda t}\vec{v}$.

We need the eigenvector $\vec{v}$ for $\lambda=i$ (and its conjugate $\vec{\bar{v}}$ for $\lambda=-i$).

Solve the equation $(A-\lambda I)\vec{v}=\vec{0}$ for $\lambda=i$:

$$\begin{pmatrix}-i&-1 & | & 0\\ 1&-i & | & 0\end{pmatrix} \xrightarrow{iR_{2}+R_{1}} \begin{pmatrix}0&0 & | & 0\\ 1&-i & | & 0\end{pmatrix}$$

The second row implies $v_1 - i v_2 = 0$, so $v_1 = i v_2$. If we set $v_2=1$, then $v_1=i$.

The eigenvector is **complex**:

$$\vec{v}=\begin{pmatrix}i\\ 1\end{pmatrix}$$

By repeating the procedure (or using the property of complex conjugates), the eigenvector for $\lambda=-i$ is:

$$\vec{v}=\begin{pmatrix}-i\\ 1\end{pmatrix}$$

The eigenvalue/eigenvector pairs are:

$$\lambda = i \Rightarrow \vec{v}=\begin{pmatrix}i\\ 1\end{pmatrix} \quad \text{and} \quad \lambda = -i \Rightarrow \vec{v}=\begin{pmatrix}-i\\ 1\end{pmatrix}$$

These are always **complex conjugate pairs** ($\lambda$ and $\bar{\lambda}$, $\vec{v}$ and $\vec{\bar{v}}$). We can never have an odd number of complex eigenvalues.

Complex Solutions and Real Parts

Solution 1 ($\vec{x}^{(1)}$)

Using $\lambda=i$ and $\vec{v}=\begin{pmatrix}i\\ 1\end{pmatrix}$:

$$\vec{x}^{(1)}=e^{it}\begin{pmatrix}i\\ 1\end{pmatrix}$$

Using Euler's formula, $e^{it}=\cos(t)+i\sin(t)$:

$$\vec{x}^{(1)}=(\cos(t)+i\sin(t))\begin{pmatrix}i\\ 1\end{pmatrix}$$ $$\vec{x}^{(1)}=\begin{pmatrix}i\cos(t)-\sin(t)\\ \cos(t)+i\sin(t)\end{pmatrix}$$

Separating the real and imaginary parts:

$$\vec{x}^{(1)} = \underbrace{\begin{pmatrix}-\sin(t)\\ \cos(t)\end{pmatrix}}_{\text{Real part } \vec{u}} + i\underbrace{\begin{pmatrix}\cos(t)\\ \sin(t)\end{pmatrix}}_{\text{Imaginary part } \vec{w}}$$

Solution 2 ($\vec{x}^{(2)}$)

Using $\lambda=-i$ and $\vec{v}=\begin{pmatrix}-i\\ 1\end{pmatrix}$:

$$\vec{x}^{(2)}=e^{-it}\begin{pmatrix}-i\\ 1\end{pmatrix}$$

Since $\cos(-t)=\cos(t)$ and $\sin(-t)=-\sin(t)$, $e^{-it}=\cos(t)-i\sin(t)$:

$$\vec{x}^{(2)}=(\cos(t)-i\sin(t))\begin{pmatrix}-i\\ 1\end{pmatrix}$$ $$\vec{x}^{(2)}=\begin{pmatrix}-i\cos(t)-\sin(t)\\ \cos(t)-i\sin(t)\end{pmatrix}$$ $$\vec{x}^{(2)}=\begin{pmatrix}-\sin(t)\\ \cos(t)\end{pmatrix} + i\begin{pmatrix}-\cos(t)\\ -\sin(t)\end{pmatrix}$$

Note that $\vec{x}^{(2)}$ is the **complex conjugate** of $\vec{x}^{(1)}$:

$$\vec{x}^{(2)} = \begin{pmatrix}-\sin(t)\\ \cos(t)\end{pmatrix} - i\begin{pmatrix}\cos(t)\\ \sin(t)\end{pmatrix} = \vec{u} - i\vec{w}$$

This is a complex conjugate pair again.

Fundamental Real Solutions

We want the solutions to be **real-valued** (no $i$).

The real and imaginary parts of $\vec{x}^{(1)}$ are:

$$\vec{u}(t)=\begin{pmatrix}-\sin(t)\\ \cos(t)\end{pmatrix} \quad \text{and} \quad \vec{w}(t)=\begin{pmatrix}\cos(t)\\ \sin(t)\end{pmatrix}$$

It can be verified that $\vec{u}(t)$ and $\vec{w}(t)$ are both real-valued solutions to $\vec{x}'=\begin{pmatrix}0&-1\\ 1&0\end{pmatrix}\vec{x}$:

$$\vec{u}'(t)=\begin{pmatrix}-\cos(t)\\ -\sin(t)\end{pmatrix}$$ $$A\vec{u}(t) = \begin{pmatrix}0&-1\\ 1&0\end{pmatrix}\begin{pmatrix}-\sin(t)\\ \cos(t)\end{pmatrix}=\begin{pmatrix}-\cos(t)\\ -\sin(t)\end{pmatrix}$$ $$\text{Since } \vec{u}' = A\vec{u}, \text{ it is a solution.}$$

They are also **linearly independent**. The Wronskian $W$ is:

$$W= \begin{vmatrix}-\sin(t) & \cos(t)\\ \cos(t) & \sin(t)\end{vmatrix} = (-\sin(t))(\sin(t)) - (\cos(t))(\cos(t)) = -(\sin^2(t) + \cos^2(t)) = -1 \ne 0$$

Therefore, the **real and imaginary parts** of either complex solution form the **fundamental solutions**.

General Solution (Example 1)

The general solution is a linear combination of the fundamental solutions:

$$\vec{x}(t)=c_{1}\begin{pmatrix}-\sin(t)\\ \cos(t)\end{pmatrix}+c_{2}\begin{pmatrix}\cos(t)\\ \sin(t)\end{pmatrix}$$

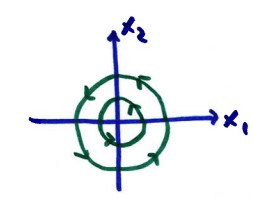
Solution curves are ovals as seen in the direction field

In the phase plane ($x_1$ vs. $x_2$), the solutions are circles or ovals. The origin is a **center**.

Example 2: Spiral Source/Sink

Example 2

Consider another system:

$$\vec{x}'=\begin{pmatrix}1&1\\ -1&1\end{pmatrix}\vec{x}$$

The eigenvalues and eigenvectors are:

$$\lambda=1 \pm i \quad \text{and} \quad \vec{v}=\begin{pmatrix}1\\ i\end{pmatrix}, \begin{pmatrix}1\\ -i\end{pmatrix}$$

We form one complex solution using $\lambda=1+i$ and $\vec{v}=\begin{pmatrix}1\\ i\end{pmatrix}$:

$$\vec{x}^{(1)}=e^{(1+i)t}\begin{pmatrix}1\\ i\end{pmatrix}$$

Using $e^{(1+i)t} = e^t e^{it} = e^t(\cos(t)+i\sin(t))$:

$$\vec{x}^{(1)}=e^{t}(\cos(t)+i\sin(t))\begin{pmatrix}1\\ i\end{pmatrix}$$ $$\vec{x}^{(1)}=e^{t}\begin{pmatrix}\cos(t)+i\sin(t)\\ i\cos(t)-\sin(t)\end{pmatrix}$$

Separating into real and imaginary parts gives the fundamental solutions ($\vec{u}$ and $\vec{w}$):

$$\vec{x}^{(1)}=e^{t}\begin{pmatrix}\cos(t)\\ -\sin(t)\end{pmatrix}+i e^{t}\begin{pmatrix}\sin(t)\\ \cos(t)\end{pmatrix}$$

The two fundamental solutions are:

$$\vec{x}^{(A)} = e^{t}\begin{pmatrix}\cos(t)\\ -\sin(t)\end{pmatrix} \quad \text{and} \quad \vec{x}^{(B)} = e^{t}\begin{pmatrix}\sin(t)\\ \cos(t)\end{pmatrix}$$

General Solution and Phase Plane (Example 2)

The general solution is:

$$\vec{x}=c_{1}e^{t}\begin{pmatrix}\cos(t)\\ -\sin(t)\end{pmatrix}+c_{2}e^{t}\begin{pmatrix}\sin(t)\\ \cos(t)\end{pmatrix}$$

The term $e^{t}$ causes the ovals to **grow** as $t$ increases, resulting in **spirals**.

In this case, since the real part of the eigenvalue ($\alpha=1$) is **positive**:

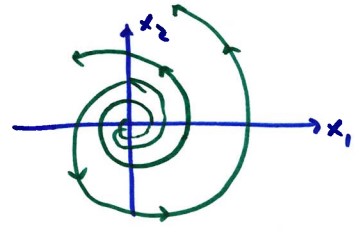
Solution curves are counterclockwise spirals that move away from the origin

The origin is a **Spiral Source** (spirals move outward as $t \to \infty$).
If the real part was **negative** ($\alpha < 0$), the origin would be a **Spiral Sink** (spirals move inward as $t \to \infty$).
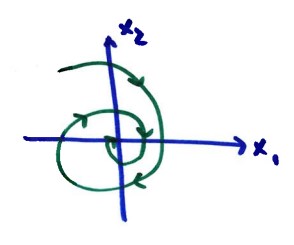
The $e^{\alpha t}$ factor comes from the **real part** of the complex eigenvalues ($\lambda = \alpha \pm i\beta$).

7.8 Repeated Eigenvalues

Case 1: Complete Matrix (Diagonalizable)

Consider the system:

$$\vec{x}'=\begin{pmatrix}1&0\\ 0&1\end{pmatrix}\vec{x}$$

The eigenvalue is $\lambda=1$, which has an **algebraic multiplicity of two**.

The eigenvector equation $(A-\lambda I)\vec{v}=\vec{0}$ is:

$$\begin{pmatrix}0&0\\ 0&0\end{pmatrix}\vec{v}=\vec{0} \quad \text{where } \vec{v}=\begin{pmatrix}v_{1}\\ v_{2}\end{pmatrix}$$

Both $v_1$ and $v_2$ are free variables. The general form of the eigenvector is:

$$\vec{v}=\begin{pmatrix}v_{1}\\ v_{2}\end{pmatrix}=v_{1}\begin{pmatrix}1\\ 0\end{pmatrix}+v_{2}\begin{pmatrix}0\\ 1\end{pmatrix}$$

We get **two linearly independent eigenvectors** ($\begin{pmatrix}1\\ 0\end{pmatrix}$ and $\begin{pmatrix}0\\ 1\end{pmatrix}$). The **geometric multiplicity is two**.

If **algebraic multiplicity = geometric multiplicity**, the matrix is called **complete** (or diagonalizable).

The solution is formed normally:

$$\vec{x}=c_{1}e^{t}\begin{pmatrix}1\\ 0\end{pmatrix}+c_{2}e^{t}\begin{pmatrix}0\\ 1\end{pmatrix}$$

Case 2: Defective Matrix (Incomplete)

The previous case produces a phase plane portrait called a **star node**.

Now, let's look at a different system:

$$\vec{x}'=\begin{pmatrix}1&1\\ 0&1\end{pmatrix}\vec{x}$$

The eigenvalue is $\lambda=1$ (repeated), so the **algebraic multiplicity is two**.

The eigenvector equation $(A-\lambda I)\vec{v}=\vec{0}$ is:

$$\begin{pmatrix}0&1 & | & 0\\ 0&0 & | & 0\end{pmatrix}\vec{v}=\vec{0}$$

The first row implies $v_2 = 0$. The general form of the eigenvector is $\vec{v}=\begin{pmatrix}v_{1}\\ 0\end{pmatrix}=v_{1}\begin{pmatrix}1\\ 0\end{pmatrix}$.

We only find **one linearly independent eigenvector** ($\begin{pmatrix}1\\ 0\end{pmatrix}$). The **geometric multiplicity is one**.

If **geometric multiplicity < algebraic multiplicity**, the matrix is **defective** (or incomplete).

The first solution is:

$$\vec{x}^{(1)}=e^{\lambda t}\vec{v}=e^{t}\begin{pmatrix}1\\ 0\end{pmatrix}$$

A second, linearly independent solution ($\vec{x}^{(2)}$) must be found using a generalized eigenvector.

End of Lesson 35 (7.6 & 7.8)