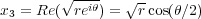
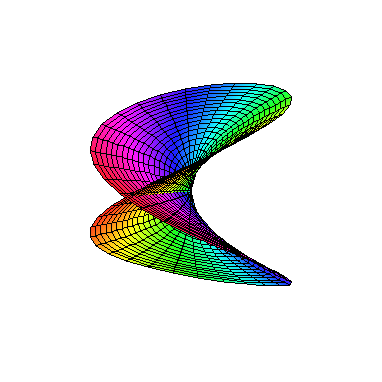
As a warm up, we start with a standard example y2 = x. When x,y are treated as real variables, this is simply a parabola opening sideways. Things get more interesting when the variables are allowed to take complex values. Since the graph would live in 2 complex or 4 real dimensions, it is impossible visualize completely. Nevertheless, we can get a sense of it projecting to 3 real dimensions, by setting x1 and x2 to be real and imaginary parts of x, and x3 to be the real part of y. ( We will use xi as coordinates of R3.) In polar coordinates, this gives
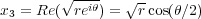
In general, a conic is given by a quadratic equation f(x,y) = 0. The standard classification that one learns in highschool becomes simpler over the complex numbers, because now there is no difference between an ellipse and a hyperbola. To clarify this, we say that two conics are equivalent if we can transform one to the other by an affine transformation
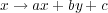

We want to give a complex plot of the circle. We start with the usual parameterization
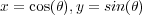
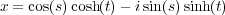
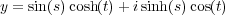
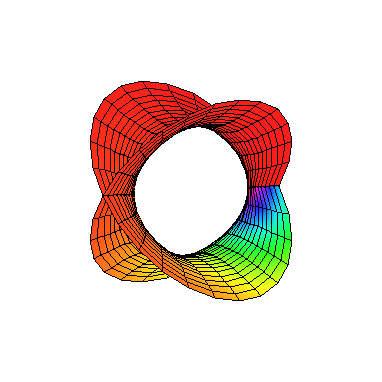

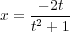
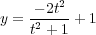
We didn’t use these formulas for the plotting, because they are less convenient (we would need t = ∞ to complete the circle). However, it has other uses. Suppose that we wanted find all right angle triangles with integer sides. By Pythagoreas’ theorem, this equivalent to finding positive integer solutions for a2 + b2 = c2. Via the substitution x = a∕c, y = b∕c, this is amounts to finding points on the circle with positive rational coordinates. Here’s a very simple procedure: Choose a rational number -1 < t < 0, and substitute into the above formulas.