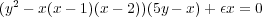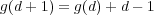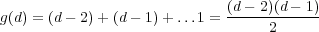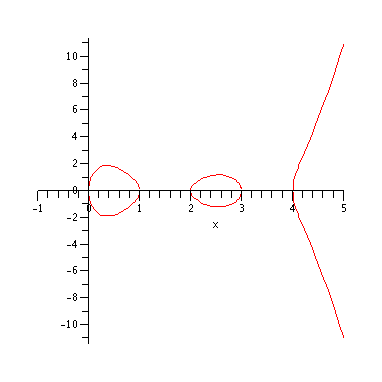We have seen how to construct spheres and tori along with various
singular objects. We now want to consider curves with large genus (i.e. many
holes). A genus two surface or "two-holed doughnut" is depicted below
 The basic idea would be to use higher degree equations.
Consider the quartic equation
The basic idea would be to use higher degree equations.
Consider the quartic equation
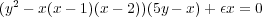 For small nonzero ε this is gives the nonsingular curve
graphed in red. However, when ε =0, this is a reducible curve which is
a union of a nonsingular cubic (blue) and a line (green).
For small nonzero ε this is gives the nonsingular curve
graphed in red. However, when ε =0, this is a reducible curve which is
a union of a nonsingular cubic (blue) and a line (green).
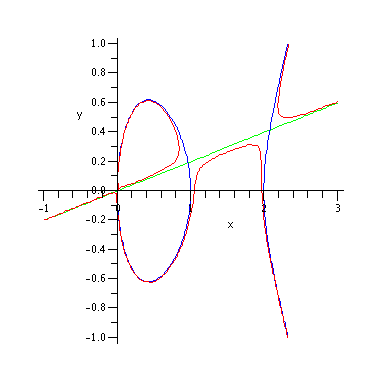 When the points of infinity are added, we get a line meeting the cubic
in 3 points.
The complex picture of this reducible curve looks something like this:
When the points of infinity are added, we get a line meeting the cubic
in 3 points.
The complex picture of this reducible curve looks something like this:
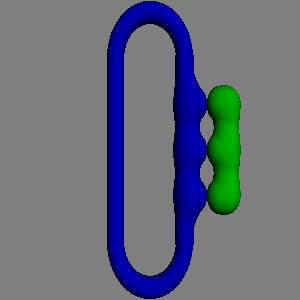 As ε changes to nonzero values, the
points of contact "open up" into tubes resulting in a genus 3 curve.
As ε changes to nonzero values, the
points of contact "open up" into tubes resulting in a genus 3 curve.
 In general if g(d) is the genus of a degree d nonsingular curve, then proceeding as
above, we obtain a nonsingular genus d
+1 curve by
"smoothing" the union of a genus d curve
and a line. The line meets the degree d curve
in d points, so
this leads to an inductive formula
In general if g(d) is the genus of a degree d nonsingular curve, then proceeding as
above, we obtain a nonsingular genus d
+1 curve by
"smoothing" the union of a genus d curve
and a line. The line meets the degree d curve
in d points, so
this leads to an inductive formula
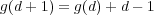 from which we get
from which we get
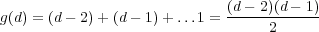 We have been a bit vague about what it means to add points at
infinity. The real answer is that we do this by working in the
projective plane, and then resolving singularities at infinity if
necessary. The above formula only applies when there are no singularities
including at infinity.
If it is necessary to resolve singularities, then the
genus of the new curve will be less than what the formula predicts.
We have been a bit vague about what it means to add points at
infinity. The real answer is that we do this by working in the
projective plane, and then resolving singularities at infinity if
necessary. The above formula only applies when there are no singularities
including at infinity.
If it is necessary to resolve singularities, then the
genus of the new curve will be less than what the formula predicts.
To get a genus 2 example, we can instead consider a
hyperelliptic curve defined by an equation y2 = p(x) where p(x) is a
polynomial of degree with at least 5 distinct roots.
The last condition guarantees it's nonsingular in C2 although it will have
singularities at infinity. In particular, the above genus formula doesn't apply,
but it can be computed by Riemann-Hurwtiz formula given in the next section. The curve
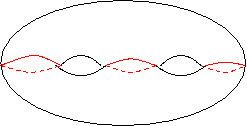
 would have genus 2. This is partly evident from the real graph:
would have genus 2. This is partly evident from the real graph:
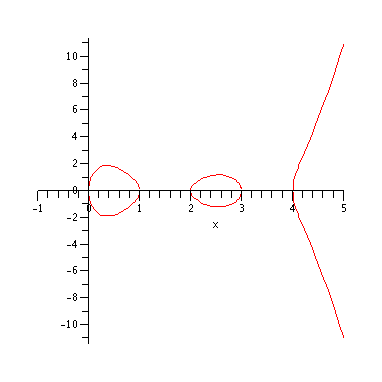 which correspond to the red curves marked on the complex picture
which correspond to the red curves marked on the complex picture
Return to first page.
Go to next page.