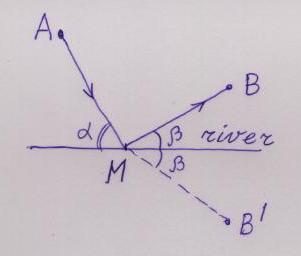
It should be clear that the shortest path will consist of two straight segments, from A to the river, and then to B. So the question is: at which point should you arrive to the river?
The answer is this: the shortest path will consist of two segments, which make EQUAL ANGLES with the river.

To see this, let M be the point where a path hits the river. Consider the point B' which is symmetric to B with respect to the river. Then AM plus MB' is a path which leads from A to B', and it has the same length as AM plus MB. Because the shortest path between A and B' is straight, the shortest path from A to B with a stop at the river will be such that AM plus MB' is straight, that is both segments of the shortest path from A to B make equal angles with the river.
It was known long ago that light behaves in a similar way. Imagine that A is a source of light, B is a receptor (your eye, for example) and the straight line R represents a mirror. Then the light, which you see as the reflection of A in the mirror, goes from A to B by two segments which lie in the same plane, perpendicular to the surface of the mirror, and these two segments make equal angles with the surface of the mirror. (You can use the Sun, a little mirror and any angle measuring instrument to check that this law holds). Thus light "chooses the shortest path" from A to B among those paths which hit the mirror on their way.
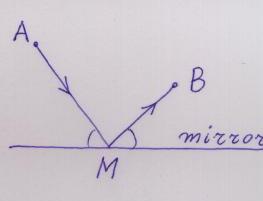
It was Hero of Alexandria who first noticed this. Probably this was the first correct observation about the nature of light. (Except the well known fact that in the absence of any obstacles or mirrors light follows a straight line.)
By the way, one does not have to assume that the river is straight (or that the mirror is flat). The shortest path (light trajectory) makes equal angles with the tangent line to the river (mirror) at the point where the path hits it.