I used to draw this curve on the blackboard in my Complex Variables courses when explaining the difference between the fundamental group and the 1-st homology group. Sometimes I had problems with my drawing which had to be a) beautiful and b) easy for students to copy.

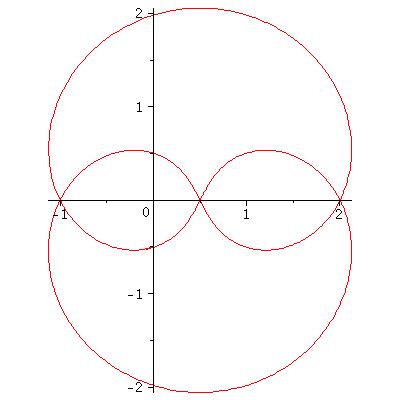
Now I have a true (canonical) shape of this curve: the hyperbolic geodesic in the twice punctured plane (at 0 and 1) in the free homotopy class of the commutator of the loops around punctures:

picture

Also helps in explaining what's a non-commutative group to children.