Chasing a U-boat

1. Problem

One cool morning in the Atlantic, as the fog clears, a destroyer and an enemy submarine suddenly spot each other at the distance of 3 nautical miles. The submarine dives immediately, her captain chooses a random direction and sails straight at his maximal speed of 10 knots (1 knot=1 nautical mile per hour) at some fixed depth, not very deep. (The captain of the submarine just follows the instructions; when submerged he has no means to find out where the destroyer is.)

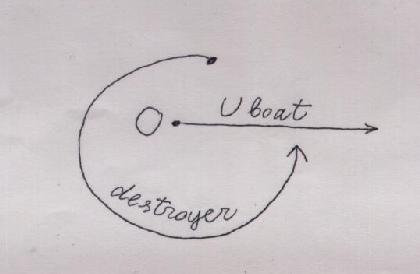
The captain of the destroyer, whose maximal speed is 20 knots, also acts according to his manual: to follow a path which will bring him for sure to a position strictly above the submarine. (In such position he can detect the submarine with his acoustic device, and release his depth charges upon it. The acoustic submarine detector has very limited range.) The destroyer captain knows* of the submarine's tactic and her maximal speed. The only thing he does not know is the random direction chosen by the submarine's captain. What path should the destroyer follow to be sure that at some moment he will be exactly above the submarine?

*If you are curious, where does he know this from, see reference [5] in the end of this article.

2. Important hint

A part of the instruction given to the captain of the destroyer reads:

A. Let O be the point where the submarine was spotted and submerged.
B. Wait still until the submarine's distance from O, which we denote OS will be equal to your distance from O, which we denote OD. (So in the accident described above he has to wait 3/10 of an hour=18 min).
C. Follow a spiral-shaped curve around O, going around and away from O, such that OD=OS all the time.
D. Before you complete one full turn around O your path will intersect the submarine's path. At this moment you will be exactly above the submarine.
E. At this moment you will detect it; as soon as this happens, release the depth charges.

So it remains to solve the following geometric problem: find a path (=parametrized curve) x=x(t), y=y(t) of the speed 20, so that the distance from the point (x,y) to the origin is OS(t)=10t all the time. Write a differential equation and solve it to complete the instruction for the destroyer's captain. Solution.

Comments about science and submarine warfare

Few people realize that research in the submarine warfare is one of the major topics of the XX century science. As I can judge, the above problem stems from the times of WWI. Probably the tactics described were actually used at that time.

`U-boat' is a common English abbreviation for the German word `Unterseeboot'. During both World Wars the Germans tried to defeat Britain by cutting the US-British transatlantic supply lines, using the submarine warfare. Both times they `almost won' this `Battle of the Atlantic', but then lost it.

The US Navy entered the WWII unprepared. The Germans could send their U-boats even to the coastal waters of the US to disrupt the trade with Central and South America with impunity. People in Florida beaches could see the terrifying scenes of burning ships torpedoed by the U-boat near the shore. In certain periods in 1942 and 1943 the situation was quite disastrous: the Germans sank more ships per month than British and Americans could build.

The US Navy mobilized scientists to solve the problem. As I can judge, this was a research project, comparable in scale with making of the nuclear bomb. As in the case of the nuclear bomb, a lot of useful science came out of this. Like the `Operations research', for example. Some of this research made during the war is probably still classified. But you can read a lot of interesting things in the books listed below. There are also some books, written by participants on the other side of the conflict, like admirals Donitz and Roeder, but I have not read them. The human aspect of the U-boat war is reflected in a popular German movie `Das Boot' (The Boat).

The research in submarine warfare was important also during the Cold War. I guess that more money and resources was spent on this research than on all fundamental science combined.

Sources: 1. V. V. Amel'kin, Differential Equations in Applications,
            Moscow, 1987 (in Russian).
         2. Samuel Morison, The Battle of the Atlantic,
            September 1939-May 1943, Boston: Little, Brown, 1947
         3. Samuel Morison, The Atlantic Battle won, May 1943-May 1945,
            Boston: Little, Brown, 1956.
         4. Thomas Korner, Pleasures of counting, Cambridge, 1996.
         5. David Kahn, Seizing the Enigma. The race to break the 
            German U-boat codes, 1939-1943, Arrow, London, 1991.