Lying over theorem
Disclaimer: in all that follows we will assume that rings are commutative rings with unity and that ring maps preserve the identity element.
A map of rings \(A\subset B\) is an integral extension provided that every element of \(B\) can be written as solution to a monic polynomial with coefficients in \(A\), i.e., for all \(b\in B\) there exists \(a_0,\dots,a_{n-1}\in A\) such that
\[ 0=b^n+a_{n-1}b^{n-1}+a_{n-2}b^{n-2}+\cdots+a_1b+a_0. \]Suppose we are given a map of rings \(\phi\colon A\to B\), a prime ideal \(\mathfrak{p}\subset A\), and a prime ideal \(\mathfrak{q}\subset B\). Then we say that \(\mathfrak{q}\) lies over \(\mathfrak{p}\) if \(\mathfrak{p}=\phi^{-1}(\mathfrak{q})\). In this case we may also say that \(\mathfrak{p}\) lies under \(\mathfrak{q}\).
Now we say that \(\phi\colon A\to B\) has the lying over property provided that given for any prime ideal \(\mathfrak{p}\subset A\) there exists a prime ideal \(\mathfrak{q}\subset B\) which lies over \(\mathfrak{p}\). If \(f\colon \text{Spec}B\to\text{Spec}A\) is the induced map on affine schemes, i.e., \(f(\mathfrak{q})=\phi^{-1}(\mathfrak{q})\), then \(A\to B\) having the lying over property is equivalent to \(f\) being a surjective map.
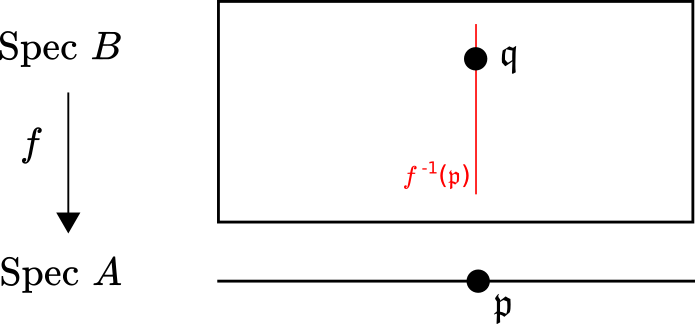
The classical lying over theorem can now be stated in geometrical language:
Theorem (Lying over): Suppose that \(A\subset B\) is an integral extension of rings, then the induced map on affine schemes \(f\colon\text{Spec}B\to\text{Spec}A\) is surjective.
Proof. We will view \(f\colon\text{Spec}B\to\text{Spec}A\) as a parameterization of \(\text{Spec}B\) by the primes of \(\text{Spec}A\). If you are unfamiliar with this idea, then all I mean is that for each prime \(\mathfrak{p}\in\text{Spec} A\) we have the corresponding fibre \(f^{-1}(\mathfrak{p})\) in \(\text{Spec}B\). The underlying set of primes of \(\text{Spec}B\) can be constructed as the union of all the fibres.
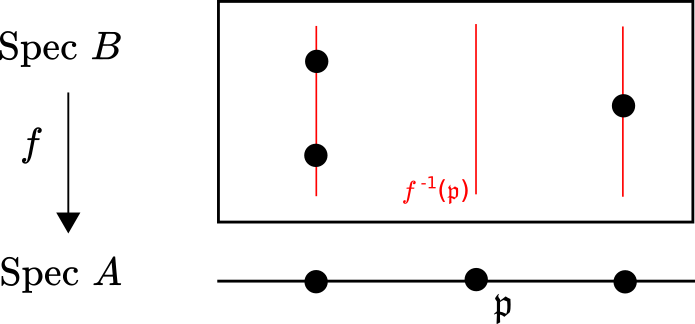
Since we are trying to show that \(f\) is surjective, one strategy would be to show that for arbitrary \(\mathfrak{p}\in\text{Spec}A\) the fibre \(f^{-1}(\mathfrak{p})\) is not empty. A bit of algebraic geometry tells us that the fibre actually has a scheme structure and that:
\[ f^{-1}(\mathfrak{p})=\text{Spec}(B\otimes_A A_{\mathfrak{p}}/\mathfrak{p}A_{\mathfrak{p}}) \]Hence if we want to show that \(f^{-1}(\mathfrak{p})\) is nonempty, then we would have to show that \(B\otimes_A A_{\mathfrak{p}}/\mathfrak{p}A_{\mathfrak{p}}\) is not the zero ring. Unfortunately, attacking the fibre directly like this is too hard. Instead we will pick out a known nonempty subspace of \(\text{Spec}B\) which contains the fibre. Then we will slowly shrink the subspace in such a way that it always contains the fibre and is nonempty. We will shrink until all that is left is the fibre itself. In which case we can conclude that the fibre must be nonempty.
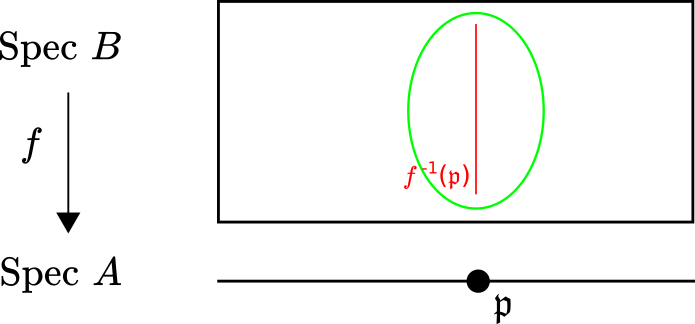
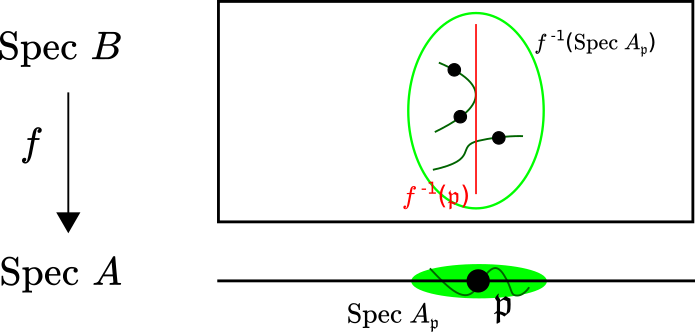
Let us construct this starting subspace of \(\text{Spec}B\). Consider the subspace
\[ \text{Spec}A_{\mathfrak{p}}=\{\mathfrak{o}\in\text{Spec}A\mid \mathfrak{o}\subset\mathfrak{p}\}\subset\text{Spec}A. \]Since \(\mathfrak{p}\in\text{Spec}A_{\mathfrak{p}}\), then \(f^{-1}(\text{Spec}A_{\mathfrak{p}})\) contains the fibre over \(\mathfrak{p}\). Again a little algebraic geometry computation tells us that
\[ f^{-1}(\text{Spec}A_{\mathfrak{p}})=\text{Spec}(B\otimes_A A_{\mathfrak{p}})=\text{Spec}B_{\mathfrak{p}}. \]Since localization is an exact functor, then \(A\subset B\) implies that \(A_{\mathfrak{p}}\subset B_{\mathfrak{p}}\). In fact more is true, since \(A\subset B\) is an integral extension, then so is \(A_{\mathfrak{p}}\subset B_{\mathfrak{p}}\). Notice that \(f\colon\text{Spec}B_{\mathfrak{p}}\to\text{Spec}A_{\mathfrak{p}}\) induces the localization map on rings \(A_{\mathfrak{p}}\subset B_{\mathfrak{p}}\).
In particular, this tells us that \(B_{\mathfrak{p}}\) is not the zero ring (assuming \(A\) and \(B\) are not both the zero ring) and consequently that the subspace \(\text{Spec}B_{\mathfrak{p}}\) is nonempty.
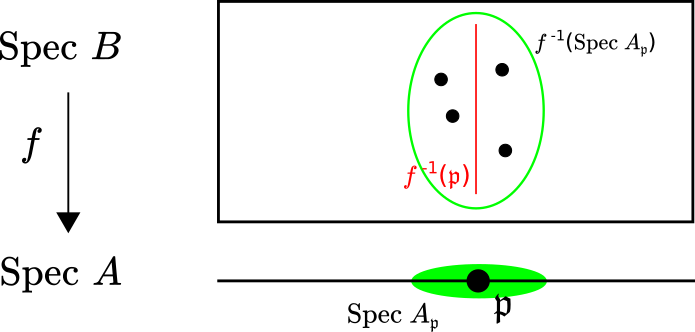
As we outlined initially, the next step is to shrink \(\text{Spec}B_{\mathfrak{p}}\) until all that is left is the fibre over \(\mathfrak{p}\). This shrinking will involve a long argument in commutative algebra. The idea will be to find the smallest variety passing through the point \(\mathfrak{p}\) of \(\text{Spec}A_{\mathfrak{p}}\) whose pullback along \(f\) is nonempty.
Let \(\Sigma\) be the set of ideals, \(I\), of \(A_{\mathfrak{p}}\) such that \(IB_{\mathfrak{p}}\ne B_{\mathfrak{p}}\). We have that the zero ideal of \(A\) is contained in \(\Sigma\). Also it may be shown that chains in \(\Sigma\) are bounded and hence by Zorn's lemma, \(\Sigma\) contains maximal elements.
Let \(I\) be such a maximal element of \(\Sigma\). Since integral extensions are compatible with quotients, then \(A_{\mathfrak{p}}/(IB_{\mathfrak{p}}\cap A_{\mathfrak{p}})\subset B_{\mathfrak{p}}/IB_{\mathfrak{p}}\) is an integral extension. The maximality of \(I\) will tell us that \(IB_{\mathfrak{p}}\cap A_{\mathfrak{p}}=I\) and hence \(A_{\mathfrak{p}}/I\subset B_{\mathfrak{p}}/IB_{\mathfrak{p}}\) is an integral extension.
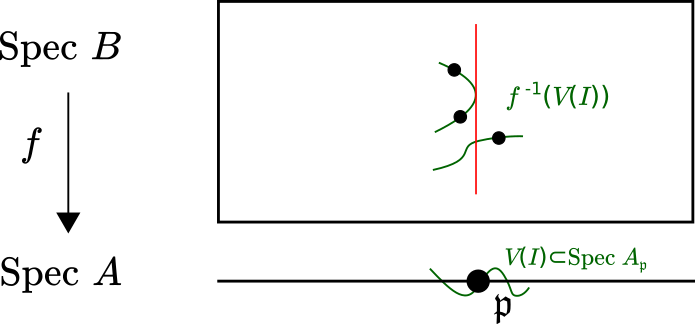
Now consider the variety \(V(I)\) in \(\text{Spec}A_{\mathfrak{p}}\). The pullback of \(V(I)\) along \(f\) is \[ f^{-1}(V(I))=\text{Spec}(B_{\mathfrak{p}}\otimes_{A_{\mathfrak{p}}}A_{\mathfrak{p}}/I)=\text{Spec}(B_{\mathfrak{p}}/IB_{\mathfrak{p}}). \]
Since \(I\in\Sigma\), then using the computation above we see that \(f^{-1}(V(I))\) is nonempty. This will be the last shrinking done in this problem, so now consider \(f\) restricted to \(f^{-1}(V(I))=\text{Spec}(B_{\mathfrak{p}}/IB_{\mathfrak{p}})\).
We claim that \(\text{Spec}(A_{\mathfrak{p}}/I)\) contains only one point. Since the pullback of this subspace is nonempty, then any prime \(\mathfrak{q}\in f^{-1}(V(I))\) maps to \(\mathfrak{p}\) under \(f\). Thus if we show the claim, then we will have that \(f\) is surjective.
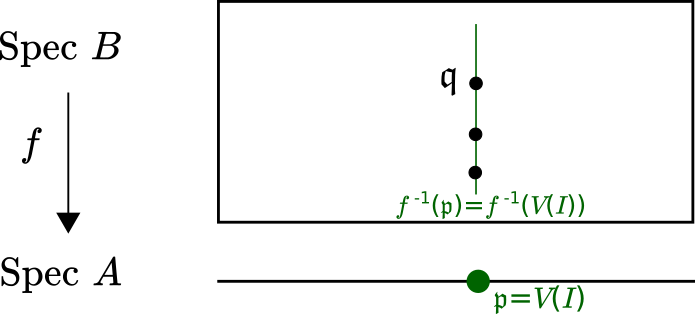
Let \(\mathfrak{p}/I\) denote the ideal in \(A_{\mathfrak{p}}/I\) which corresponds to \(\mathfrak{p}\) under the quotient map. Note that \(A_{\mathfrak{p}}/I\) is a local ring with maximal ideal \(\mathfrak{p}/I\). If \(\mathfrak{p}/I=0\), then \(A_{\mathfrak{p}}/I\) would be a field and hence \(\text{Spec}(A_{\mathfrak{p}}/I)\) is a single point.
Thus it suffices to show that \(\mathfrak{p}/I\) must always be the zero ideal. We will show this by contradiction, so assume that there exists \(a\in \mathfrak{p}-I\). The maximality of \(I\) implies that \(aB_{\mathfrak{p}}= B_{\mathfrak{p}}\). Hence there exists \(b\in B_{\mathfrak{p}}\) such that \(ab=1\). If we let bar denote the image in the quotient, then we have that \(\bar{a}\bar{b}=1\) in \(B_{\mathfrak{p}}/IB_{\mathfrak{p}}\).
Since \(A_{\mathfrak{p}}/I\subset B_{\mathfrak{p}}/IB_{\mathfrak{p}}\) is an integral extension there is an equation
\[ \bar{b}^n=a_{n-1}\bar{b}^{n-1}+\cdots+a_1\bar{b}+a_0 \]where \(a_i\in A_{\mathfrak{p}}/I\) for \(i=0,\dots,n-1\). Since \(\bar{b}^{-1}=\bar{a}\), then
\[ \bar{b}=a_{n-1}+\cdots+a_1\bar{a}^{n-2}+a_0\bar{a}^{n-1}\in A_{\mathfrak{p}}/I. \] This tells us that \(\bar{a}\) is invertible in \(A_{\mathfrak{p}}/I\). Since we assumed that \(\bar{a}\) is also in the maximal ideal of \(A_{\mathfrak{p}}/I\) we have a contradiction. Therefore, no such \(a\) exists.