Research Projects
Di Qi, MATH, PURDUE
- Reduced-order methods for statistical responses
- Statistical saturation bounds in uncertainty quantification
- Extreme event prediction using efficient models
- Statistical control of complex systems with uncertainty
- Fluid models and analysis for plasma edge turbulence
- Filtering high-dimensional turbulent dynamical systems
Back
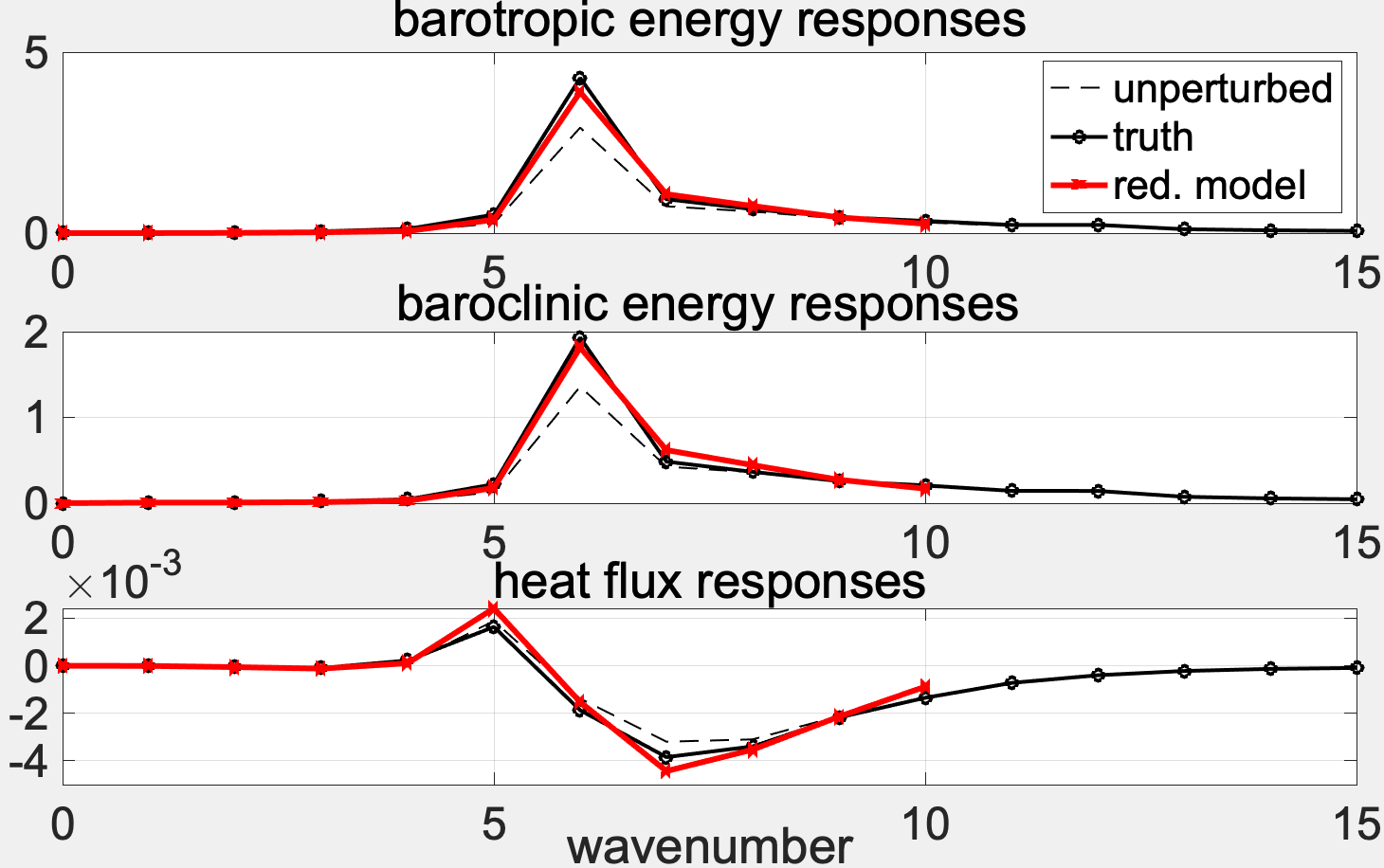
Reduced-order methods for statistical responses 
 |
Uncertainty quantification (UQ) in turbulent dynamical systems is a grand challenge whose goal is to obtain statistical estimates for key physical quantities in their nonlinear responses to changes in external forcing or uncertain initial data. For example, one issue in contemporary climate change science is the development of a systematic methodology that can recover the crucial features of the natural system in statistical equilibrium (model fidelity) and improve the imperfect model prediction skill in response to various external perturbations (model sensitivity).
We propose a general mathematical framework to construct statistically accurate reduced-order models that have skill in capturing the statistical variability in the principal directions. In the main idea of this work, there are generally three stages in the modeling strategy: imperfect model selection; calibration of the imperfect model in a training phase; and prediction of the responses to a wide class of forcing and perturbation scenarios. The methods are developed under a universal class of turbulent dynamical systems with quadratic nonlinearity. Examples in applications of the strategies to be investigated involve the climate change and controlled plasma fusion.
- Majda, A.J. and Qi, D., "Strategies for reduced-order models for predicting the statistical responses and uncertainty quantification in complex turbulent dynamical systems", SIAM Review, 60(3), pp. 491–549, 2017
- Qi, D. and Majda, A.J., "Low-dimensional reduced-order models for statistical response and uncertainty quantification: two-layer baroclinic turbulence", J. Atmos. Sci., 73(12), pp. 4609–4639, 2016
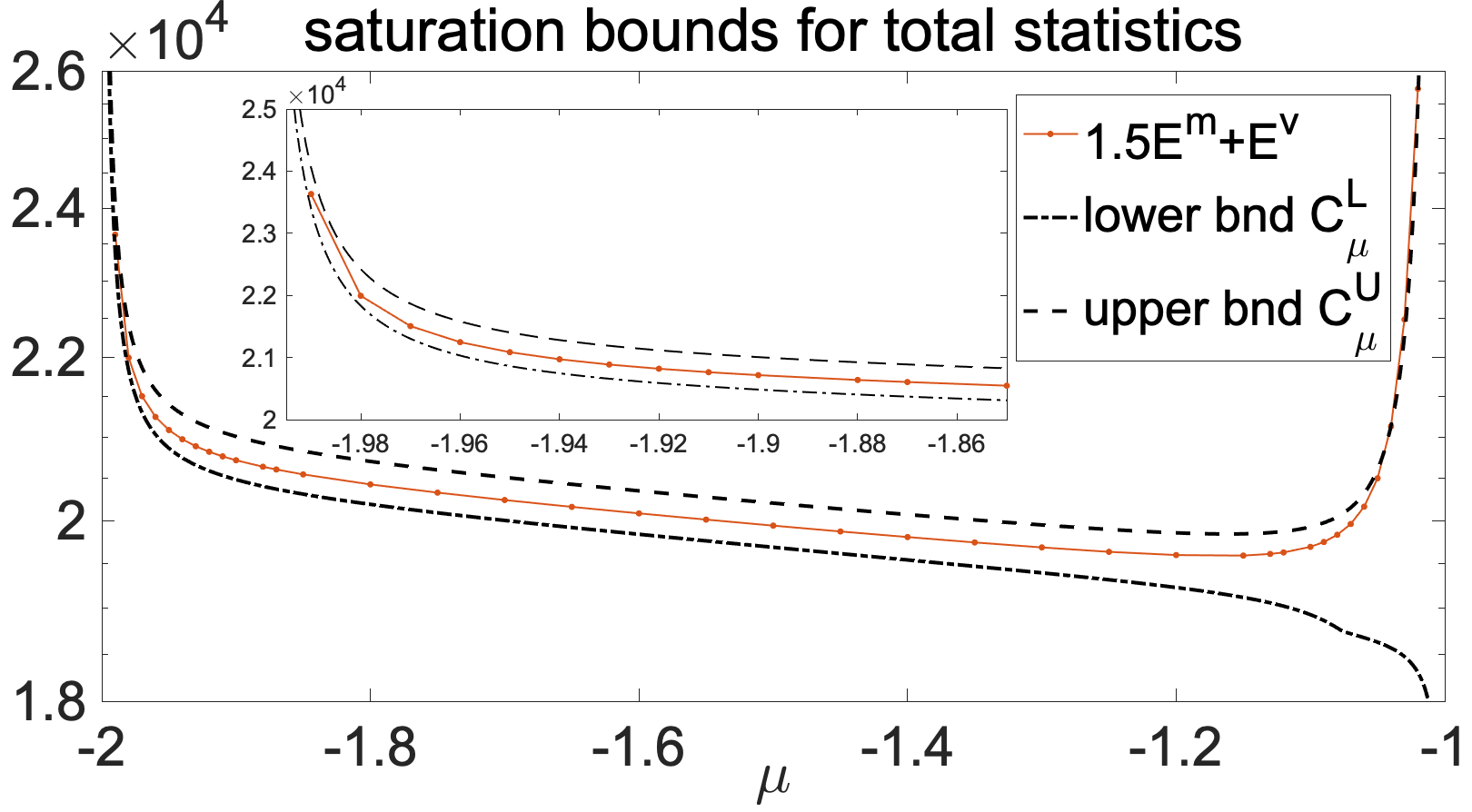
Statistical saturation bounds in uncertainty quantification 
 |
Stability theory for a time-independent steady-state solution in turbulent systems is of interest not only in theoretical investigations but also in many experimental and observational studies. Statistical ensemble prediction is an important topic in weather and climate research. The ensemble motion of trajectories introduces additional complexity into the stability analysis especially when smaller-scale motions have a significant feedback and interaction with a larger-scale mean flow.
We are studying statistical saturation of stability taking into account the time evolution of the probabilistic distribution of the state variables through an ensemble representation, different from the deterministic nonlinear stability that tracks the development of perturbations in time along one trajectory realization of the solutions. Rigorous statistical bounds controlling the total fluctuations in mean and variance are derived for typical geophysical systems. The statistical description about the system can offer a more comprehensive characterization about the nonlinear instabilities in ensemble statistics rather than only a pointwise quantification about the fluctuations in time around the steady-state attractor.
- Qi, D. and Majda, A.J., "Rigorous statistical bounds in uncertainty quantification for one-layer turbulent geophysical flows", J. Nonlinear Sci., 28(5), pp. 1709–1761, 2018
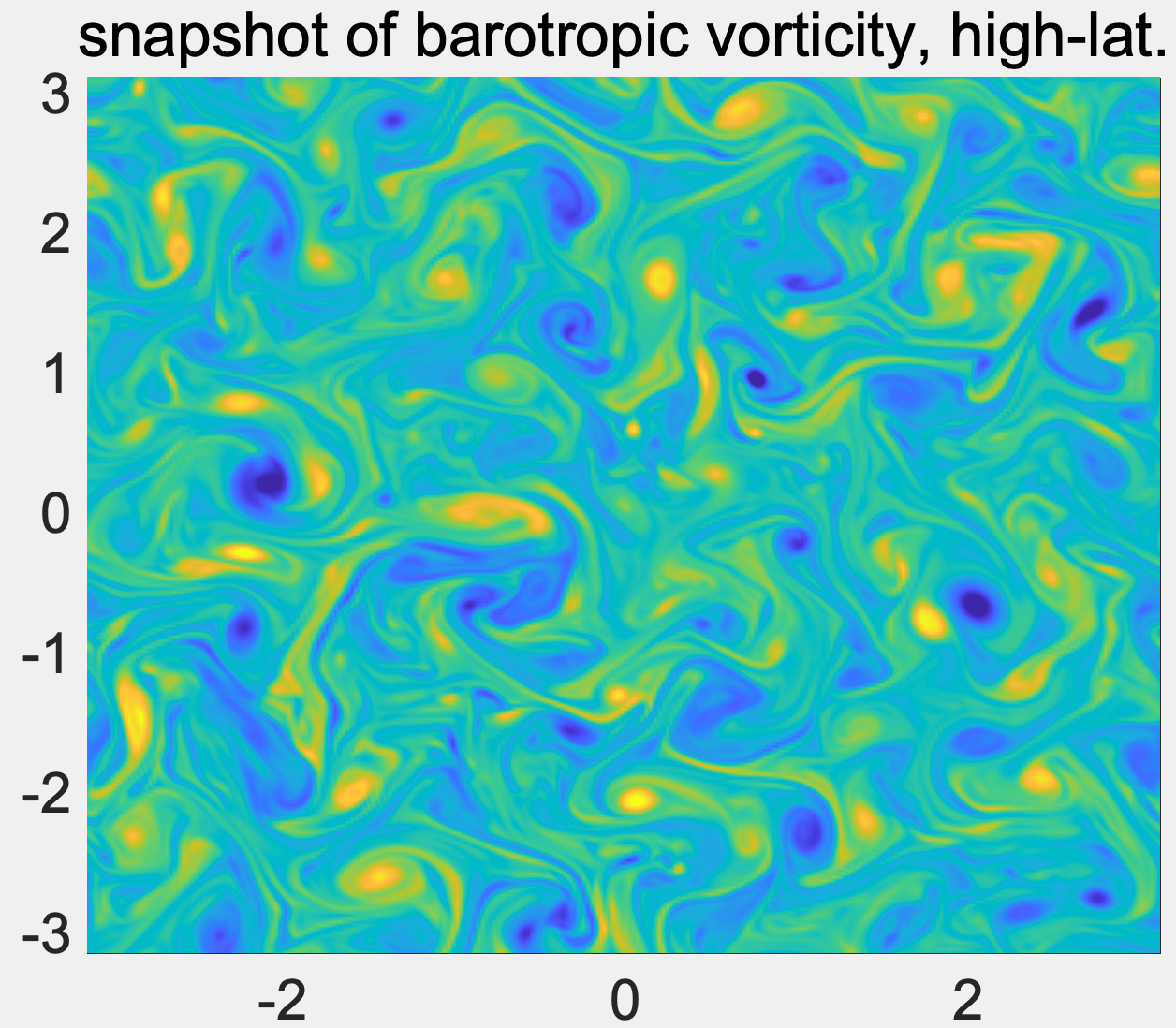
Statistical control of complex systems with uncertainty 
 |
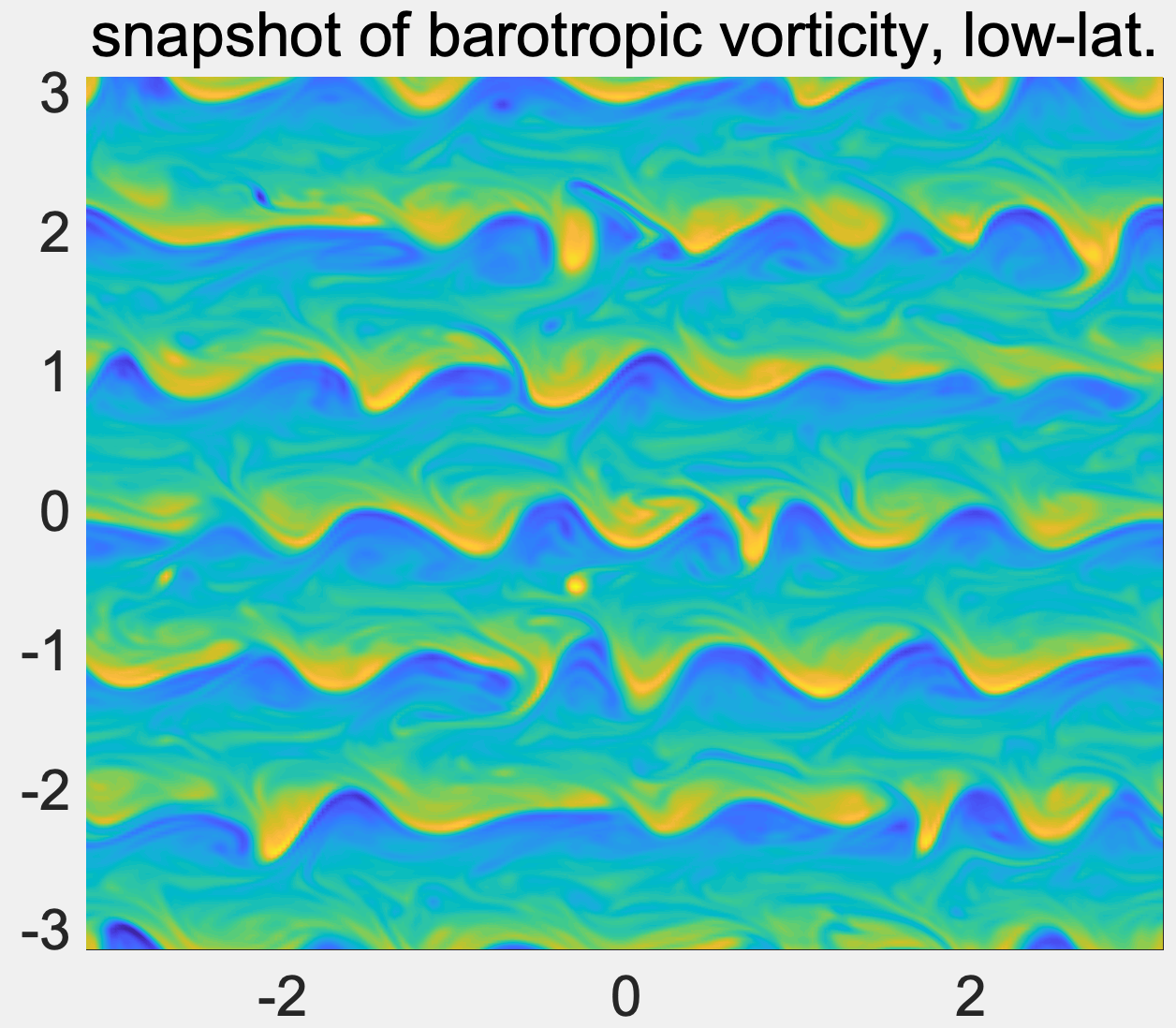 |
Many turbulent dynamical systems are characterized by a high-dimensional phase space and a large number of instabilities, including climate, material, neural science, and plasma physics. Control of complex turbulent flows is a general problem concerning about, for example, mitigation of the effects of climate change or design of technology with fully developed shear turbulence.
Solving the control problem in complex turbulent systems is challenged by difficulties of large instabilities and strong nonlinear exchange of energy among different temporal and spatial scales. The goal in our research is to propose efficient statistical control strategies for general complex turbulent systems with energy conserving nonlinearity. The effective control method is based on the statistical energy principle and linear response theory to drive perturbed statistical solutions back to a small neighborhood of the original unperturbed target statistical equilibrium state in an easy and efficient way. The proposed statistical control strategy has been verified with robust skill through numerical experiments, and has potential for extremely complex turbulent systems.
- Majda, A.J. and Qi, D., "Effective control of complex turbulent dynamical systems through statistical functionals", Proc. Natl. Acad. Sci., 114(22), pp. 5571–5576, 2017
Extreme event prediction using efficient models 
Understanding and predicting extreme events and their anomalous statistics in complex nonlinear systems is an active topic requiring qualitative and quantitative models and novel numerical algorithms. The development of simplified physically constrained stochastic and statistical models offers helpful tools for broadening our understanding for the essential physical processes.
We study the capability of using simplified stochastic and statistical models to capture crucial non-Gaussian statistics. Much simpler and more tractable models are proposed to approximate the complex and high-dimensional flow equations. The imperfect model prediction skill is improved through a judicious calibration of the model errors using leading order statistics of the background advection flow, while no additional prior information is required. One approach in our research predicts the skewed PDFs found in laboratory experiments for shallow water waves revealing a remarkable transition from Gaussian to anomalous behavior as surface water waves cross an abrupt depth change; the other direction goes to the efficient prediction of fat exponential tails in PDFs found in the passive scalar tracers advected by turbulent geophysical flows.
 |
 |
- Majda, A.J., Moore, M.N.J., and Qi, D., "A statistical dynamical model to predict extreme events and anomalous features in shallow water waves with abrupt depth change", Proc. Natl. Acad. Sci., 2018
Fluid models and analysis for plasma edge turbulence 
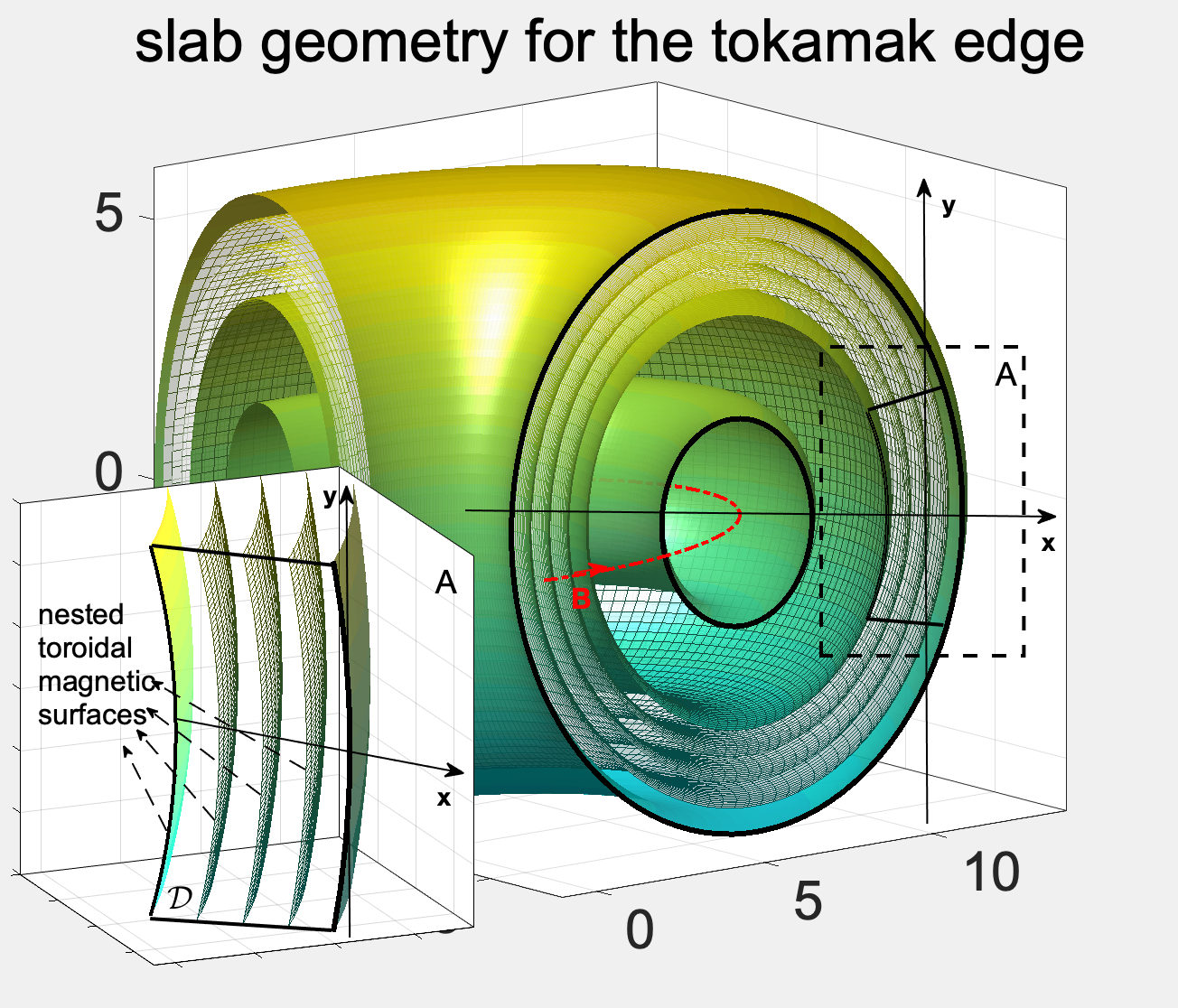 |
Interactions between zonal flows and turbulent waves are a ubiquitous phenomena in nature and the laboratory. In magnetic confinement plasmas, the interplay between zonal flows and drift wave turbulence driven by temperature and density gradients is thought to play a critical role in the observed level of heat and particle transport perpendicular to the magnetic surfaces. Reduced fluid models based on simplifying assumptions for the magnetic geometry and the plasma regime of interest have contributed to improve our understanding of the drift wave - zonal flow dynamics.
In our research, we are studying the basic mechanisms involved in the drift wave - zonal flow interacting mechanism under the light of a new set of qualitative models. Understanding this process is a critical step towards the goals of minimizing heat transport in magnetically confined plasmas and designing compact, economically viable fusion devices. We propose a new reduced fluid model for the drift wave - zonal flow dynamics. Our new model can be viewed as an extension of the classic Hasegawa-Wakatani (HW) model and is based on an improved treatment of the electron responses parallel to the field lines, to guarantee a balanced electron flux on magnetic surfaces. In the next stage, we are developing theories based on secondary instability and selective decay principle to study the creation and persistence of zonal flows widely observed in plasma edge turbulence.
- Qi, D. and Majda, A.J., "Transient metastability and selective decay for the coherent zonal structures in plasma edge turbulence", J. Nonlinear Sci., 2018
- Majda, A.J., Qi, D., and Cerfon, A.J., "A flux-balanced fluid model for collisional plasma edge turbulence: model derivation and basic physical features", Physics of Plasmas, 25(10), p.102307, 2018
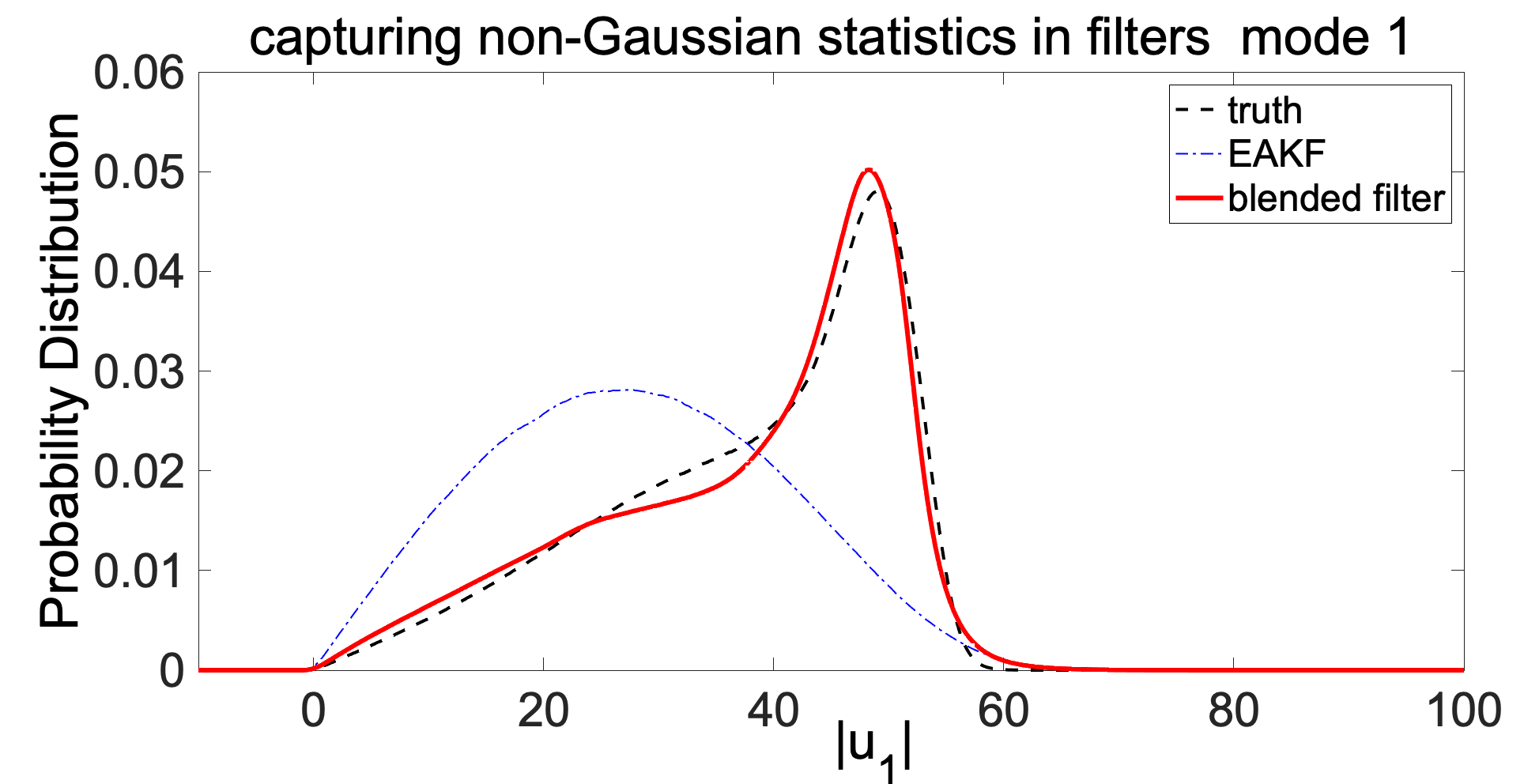
Filtering high-dimensional turbulent dynamical systems 
 |
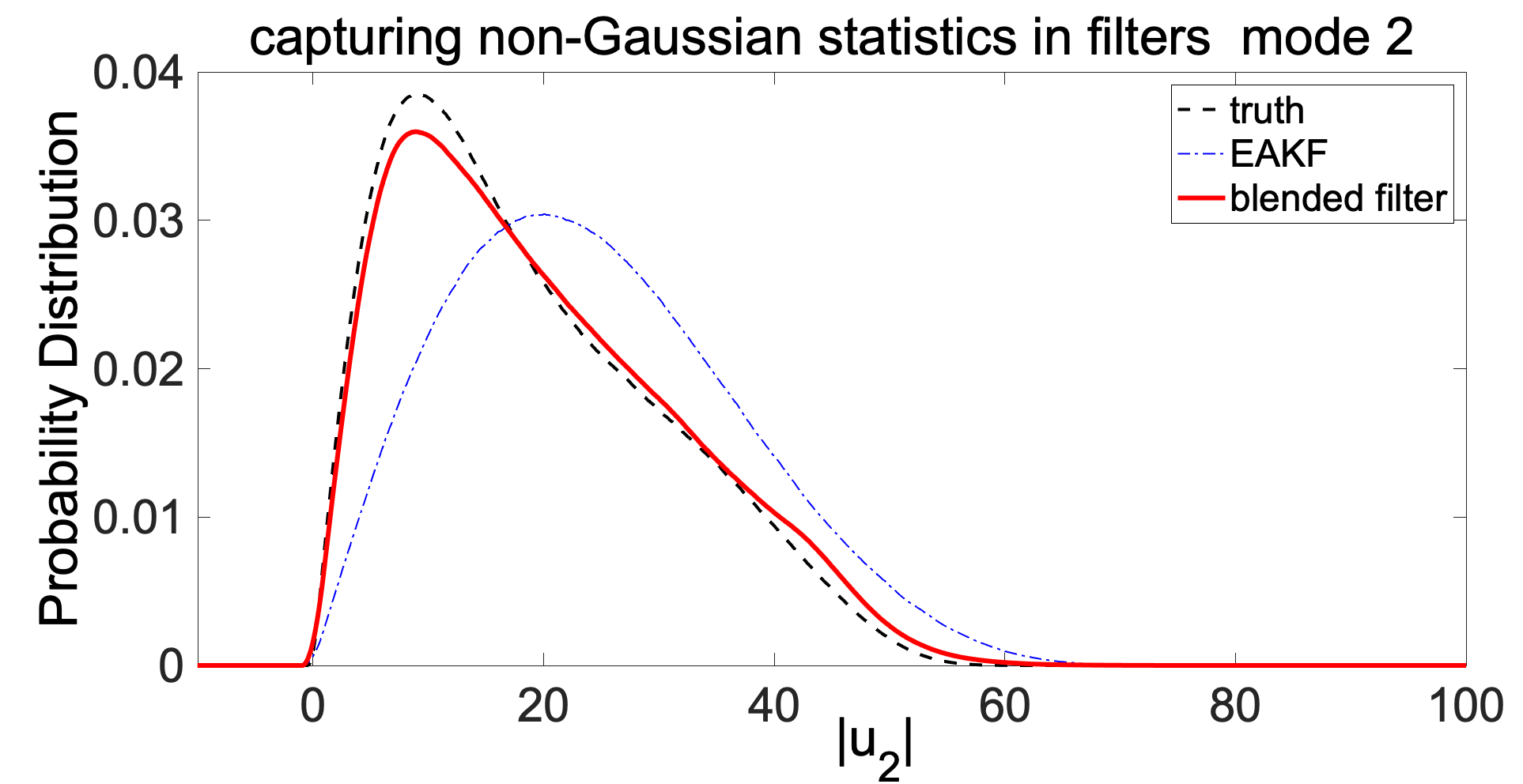 |
Filtering (or data assimilation) concerns about getting an optimal estimation for the future states of a complex system combining the information from an imperfect model prediction and noisy observation data sets from nature. For sparse, inaccurate and infrequent observations, which are typical in the available data of geophysical systems, traditional ensemble filtering methods suffer from the so-called ‘catastrophic filter divergence’ which frequently drives the filter predictions to machine infinity.
We develop a set of ensemble based filtering methods that have proved to be effective tools allowing computationally cheap, low dimensional ensemble state approximation for extremely high dimensional turbulent dynamical systems. These algorithms exploit the physical structure of turbulent dynamical systems and capture non-Gaussian features in a low dimensional subspace through particles interacting with evolving conditional Gaussian statistics on the remaining portion of the phase space. The formalism developed is shown useful for multiscale filtering of turbulent systems, such as the quasi-geostrophic model for weather prediction, and will be generalized to a larger group of systems besides the climate models.
- Qi, D. and Majda, A.J., "Blended particle methods with adaptive subspaces for filtering turbulent dynamical systems", Physica D: Nonlinear Phenomena, 298, pp. 21–41, 2015
- Majda, A.J., Qi, D., and Sapsis, T.P., "Blended particle filters for large dimensional chaotic dynamical systems", Proc. Natl. Acad. Sci., 111(21), pp. 7511–7516, 2014
