Lecture 20 & 21: Section 3.6 Forced Oscillations and Resonance

Recall: The Mass-Spring-Dashpot System

From Section 3.4, the motion of a mass-spring-dashpot system is described by the linear second-order differential equation:

$$ m x'' + c x' + k x = F(t) $$

Where $ m $ is mass, $ c $ is the damping constant, $ k $ is the spring constant, and $ F(t) $ is the external force. We focus on rotating components that produce simple harmonic external forces:

F(t) = F_0 \cos(\omega t) \quad \text{or} \quad F(t) = F_0 \sin(\omega t)

(I) Undamped Forced Oscillation

Example 1: Solving the Initial Value Problem

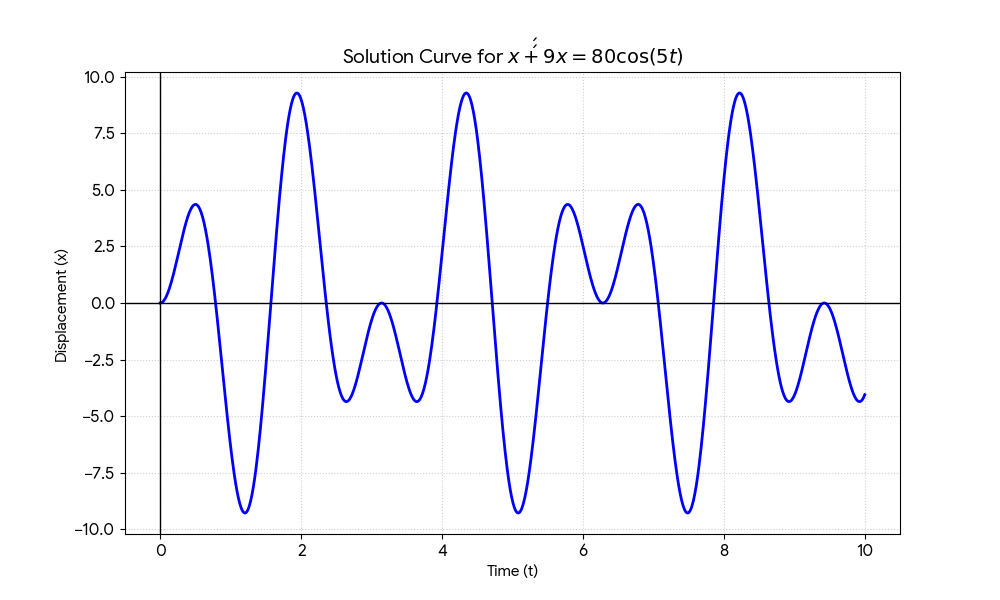
Solve $ x'' + 9x = 80 \cos(5t) $ with $ x(0) = 0, x'(0) = 0 $.

Step 1: Find the complementary function. Characteristic equation $ r^2 + 9 = 0 \implies r=3i, -3i$. $ x_c = C_1 \cos(3t) + C_2 \sin(3t) $.

Step 2: Take $x_p=A \cos(5t)$. Substituting into the equation:
$ (-25A + 9A) \cos(5t) + (-25B + 9B) \sin(5t) = 80 \cos(5t) $.
$ -16A = 80 \implies A = -5 $.
$ -16B = 0 \implies B = 0 $.
Resulting particular solution: $ x_p = -5 \cos(5t) $.

Step 3: General solution: $ x(t) = C_1 \cos(3t) + C_2 \sin(3t) - 5 \cos(5t) $.

Step 4: Solve for $ C_1 $ and $ C_2 $ to find the particular solution to the initial value problem.
$ x(0) = C_1 - 5 = 0 \implies C_1 = 5 $.
$ x'(t) = -3C_1 \sin(3t) + 3C_2 \cos(3t) + 25 \sin(5t) $.
$ x'(0) = 3C_2 = 0 \implies C_2 = 0 $.
Final form: $ x(t) = 5 \cos(3t) - 5 \cos(5t) $. Using the Sum-to-Product identity $ \cos \alpha - \cos \beta = -2 \sin \frac{\alpha - \beta}{2} \sin \frac{\alpha + \beta}{2} $:
$ x(t) = -10 \sin\left(\frac{3t-5t}{2}\right) \sin\left(\frac{3t+5t}{2}\right) = 10 \sin(t) \sin(4t) $.

A graph of the solution curve x(t) = 5cos(3t) - 5cos(5t). It shows an oscillating wave with a varying amplitude, characteristic of beats in forced undamped motion. — Figure: Forced Undamped Motion displaying Beats

Consider the undamped case ($ c = 0 $) with forcing function $ F(t) = F_0 \cos(\omega t) $:

m x'' + k x = F_0 \cos(\omega t)

The natural circular frequency is $ \omega_0 = \sqrt{k/m} $. The complementary solution is $ x_c = C_1 \cos(\omega_0 t) + C_2 \sin(\omega_0 t) $.

Case 1: $ \omega \neq \omega_0 $

Take $ x_p = A \cos(\omega t) + B \sin(\omega t) $. Then $ x_p'' = -\omega^2 A \cos(\omega t) - \omega^2 B \sin(\omega t) $. Substitute into the equation:

$$ m(-\omega^2 A \cos(\omega t) - \omega^2 B \sin(\omega t)) + k(A \cos(\omega t) + B \sin(\omega t)) = F_0 \cos(\omega t) $$

$\cos(\omega t)$ terms: $ -m\omega^2 A + k A = F_0 \implies A(k - m\omega^2) = F_0 \implies A = \frac{F_0}{k - m\omega^2} $
$\sin(\omega t)$ terms: $ -m\omega^2 B + k B = 0 \implies B(k - m\omega^2) = 0 \implies B = 0 $

Rewriting $ A $ using $ \omega_0^2 = k/m $:

$$ A = \frac{F_0/m}{k/m - \omega^2} = \frac{F_0/m}{\omega_0^2 - \omega^2}$$

The resulting general solution is designated as:

x(t) = C \cos(\omega_0 t - \alpha) + \frac{F_0/m}{\omega_0^2 - \omega^2} \cos(\omega t) \quad (1)

Finding the Particular Solution when Initial Conditions are Zero

If the mass is initially at rest at the equilibrium position ($ x(0) = 0 $ and $ x'(0) = 0 $), the constants are: $$ C_1 = -\frac{F_0}{m(\omega_0^2 - \omega^2)}, \quad C_2 = 0 $$

Substituting into Formula (1) gives: $$ x(t) = \frac{F_0}{m(\omega_0^2 - \omega^2)} (\cos(\omega t) - \cos(\omega_0 t)) $$ Using the product-to-sum identity, we reach the form: $$ x(t) = \frac{2F_0}{m(\omega_0^2 - \omega^2)} \sin\left(\frac{\omega_0 - \omega}{2}t\right) \sin\left(\frac{\omega_0 + \omega}{2}t\right) $$

The Phenomenon of Beats

If the external frequency $ \omega $ is close to the natural frequency $ \omega_0 $, then $ \omega_0 + \omega $ is very large compared to $ \omega_0 - \omega $. We interpret the solution $ x(t) $ as a rapid oscillation with frequency $ \frac{1}{2}(\omega_0 + \omega) $ that is constrained by a slowly varying amplitude envelope:

x(t) = A(t) \sin\left(\frac{\omega_0 + \omega}{2}t\right) \quad \text{where } A(t) = \frac{2F_0}{m(\omega_0^2 - \omega^2)} \sin\left(\frac{\omega_0 - \omega}{2}t\right)

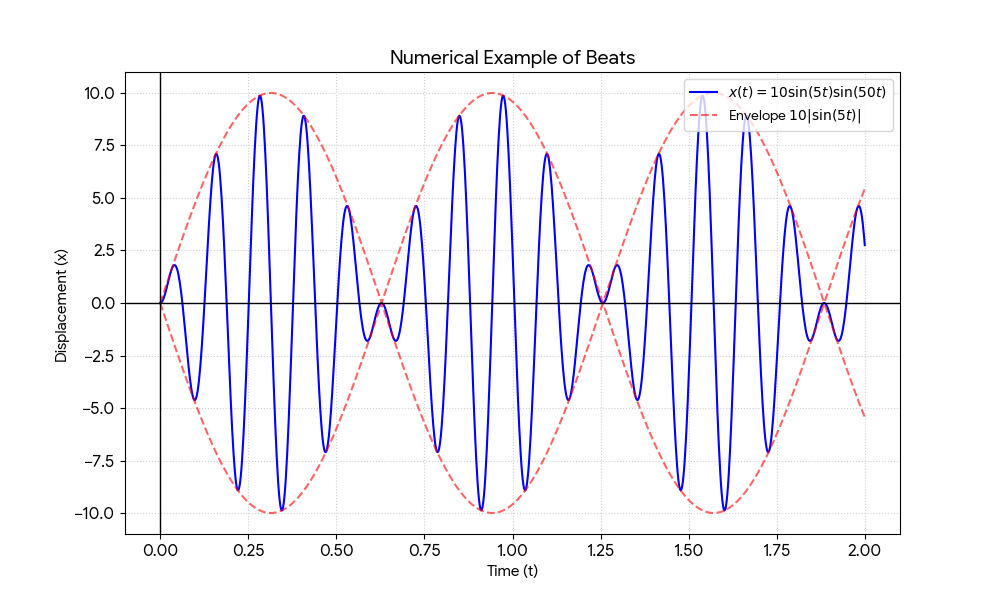
This rapid oscillation with a comparatively slowly varying periodic amplitude is called beats.

Numerical Example of Beats:
Consider a system where $ m = 0.1 $, $ F_0 = 50 $, $ \omega_0 = 55 $, and $ \omega = 45 $. The position function becomes: $$ x(t) = 10 \sin(5t) \sin(50t) $$

A graph showing the beats phenomenon. A high-frequency sine wave is contained within a slower-oscillating sine wave envelope, causing the total amplitude to periodically increase and decrease. — Figure: Beats for x(t) = 10 sin(5t) sin(50t)

Resonance Analysis

The particular solution amplitude can be written as $ A = \pm \frac{\rho F_0}{k} $, where $ \rho $ is the amplification factor:

\rho = \frac{1}{|1 - (\omega/\omega_0)^2|}

As the external frequency $ \omega $ approaches the natural frequency $ \omega_0 $, the amplification factor $ \rho $ and the amplitude increase without bound. This is the phenomenon of resonance.

Case 2: $ \omega = \omega_0 $ (Pure Resonance)

In this case, the external frequency matches the natural frequency. The trial solution must be modified to avoid duplication with the complementary solution:
Guess $ x_p = t(A \cos(\omega_0 t) + B \sin(\omega_0 t)) $. The derivatives are:
$ x_p' = (A \cos(\omega_0 t) + B \sin(\omega_0 t)) + t(-\omega_0 A \sin(\omega_0 t) + \omega_0 B \cos(\omega_0 t)) $
$ x_p'' = -2\omega_0 A \sin(\omega_0 t) + 2\omega_0 B \cos(\omega_0 t) - \omega_0^2 t(A \cos(\omega_0 t) + B \sin(\omega_0 t)) $

Substituting into the undamped equation $ m x'' + k x = F_0 \cos(\omega_0 t) $:
$ m[-2\omega_0 A \sin(\omega_0 t) + 2\omega_0 B \cos(\omega_0 t)] = F_0 \cos(\omega_0 t) $.
Equating coefficients: $ -2m\omega_0 A = 0 \implies A = 0 $ and $ 2m\omega_0 B = F_0 \implies B = \frac{F_0}{2m\omega_0} $.

Example 2: Pure Resonance Calculation

Let $ F_0 = 100 $, $ m = 1.25 $, and $ \omega_0 = 40 $. Find the particular solution $ x_p $ for $ x'' + 40^2 x = 80 \cos(40t) $.

Step 1: Set up the trial solution. Given $ \omega = \omega_0 = 40 $, let $ x_p = t(A \cos(40t) + B \sin(40t)) $.

Step 2: Solve for coefficients. Substituting the trial solution and its derivatives into the equation and simplify to get: $$ -80A \sin(40t) + 80B \cos(40t) = 80 \cos(40t)$$ Equating terms: $ -80A = 0 \implies A = 0 $; $ 80B = 80 \implies B = 1 $.

Result: $ x_p(t) = t \sin(40t) $. The amplitude increases linearly over time.

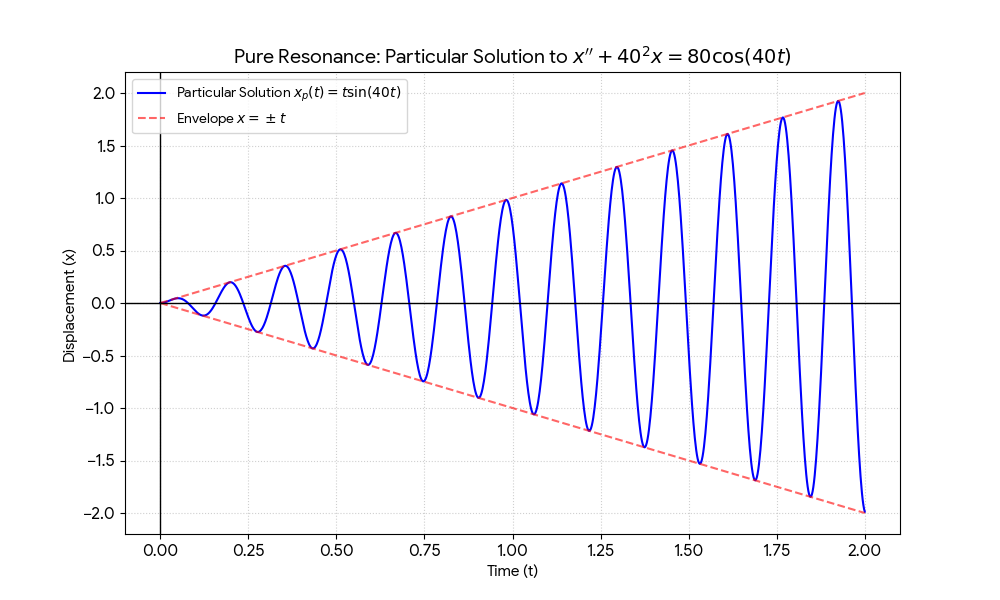
A graph of pure resonance showing a sine wave with an amplitude that increases linearly over time, bounded by the envelope x = plus or minus t. — Figure: Pure Resonance Solution $x_p(t) = t \sin(40t)$

This scenario where the amplitude grows linearly without bound is pure resonance. It represents the reinforcement of natural vibrations by externally impressed vibrations at the same frequency.

(II) Damped Forced Oscillation

Governing equation: $ m x'' + c x' + k x = F_0 \cos(\omega t) $.
The general solution is $ x = x_c + x_p $. Here $ x_c $ is the transient solution ($ x_{tr} $) because it decays to zero as $ t \to \infty $. The particular solution $ x_p $ is the steady-periodic oscillation ($ x_{sp} $).

Solving for $ A $ and $ B $ for Steady-Periodic Solutions

Assuming $ x_{sp} = A \cos(\omega t) + B \sin(\omega t) $. Substituting into the equation and equating coefficients:

$\cos(\omega t)$: $ (k - m\omega^2)A + c\omega B = F_0 $
$\sin(\omega t)$: $ -c\omega A + (k - m\omega^2)B = 0 \implies A = \frac{k - m\omega^2}{c\omega} B $

Solving the system for $ A $ and $ B $ (dependent on $\omega$):

$$ A(\omega) = \frac{(k - m\omega^2)F_0}{(k - m\omega^2)^2 + (c\omega)^2}, \quad B(\omega) = \frac{c\omega F_0}{(k - m\omega^2)^2 + (c\omega)^2} $$

The amplitude is

$$ C(\omega) = \sqrt{A^2 + B^2} = \frac{F_0}{\sqrt{(k - m\omega^2)^2 + (c\omega)^2}} $$.

Practical Resonance

Practical resonance occurs when the external frequency $ \omega $ is tuned to produce the largest possible steady-state amplitude $ C(\omega) $. This requires minimizing the denominator $ (k - m\omega^2)^2 + (c\omega)^2 $. Expanding this term:

$$ m^2 \omega^4 - (2km - c^2)\omega^2 + k^2 $$

If $ c \ge \sqrt{2km} $: $ C(\omega) $ is a steadily decreasing function; no practical resonance occurs.
If $ c < \sqrt{2km} $: Practical resonance occurs at frequency: $$ \omega = \sqrt{\frac{k}{m} - \frac{c^2}{2m^2}} < \omega_0 $$

Example 3: Damped Forced Motion

Given $ m=1, c=2, k=26, F(t) = 82 \cos(4t) $ with $ x(0)=6, x'(0)=0 $.

Step 1: Set up the Nonhomogeneous Equation.
The differential equation is: $$x'' + 2x' + 26x = 82 \cos(4t)$$

Step 2: Find the Transient Solution ($ x_{tr} $).
The associated homogeneous equation is $ x'' + 2x' + 26x = 0 $. The characteristic equation is: $$r^2 + 2r + 26 = 0 \implies r = \frac{-2 \pm \sqrt{4 - 104}}{2} = -1 \pm 5i$$ Thus, the transient solution (which decays as $ t \to \infty $) is: $$x_{tr}(t) = e^{-t}(C_1 \cos(5t) + C_2 \sin(5t))$$ We will have to determine $C_1$ and $C_2$ later.

Step 3: Find the Steady-Periodic Solution ($ x_{sp} $) using Undetermined Coefficients.
We guess a trial particular solution $ x_{sp} = A \cos(4t) + B \sin(4t) $.
Calculating its derivatives:

$ x_{sp}' = -4A \sin(4t) + 4B \cos(4t) $
$ x_{sp}'' = -16A \cos(4t) - 16B \sin(4t) $

Substituting these into the original differential equation: $$(-16A \cos(4t) - 16B \sin(4t)) + 2(-4A \sin(4t) + 4B \cos(4t)) + 26(A \cos(4t) + B \sin(4t)) = 82 \cos(4t)$$ Grouping the coefficients:

$\cos(4t)$ terms:$ -16A + 8B + 26A = 82 \implies 10A + 8B = 82 $
$\sin(4t)$ terms:$ -16B - 8A + 26B = 0 \implies -8A + 10B = 0 $

Solve the linear system to get $A=5$, $B = 4$.
The steady-periodic solution is: $$x_{sp}(t) = 5 \cos(4t) + 4 \sin(4t)$$

Convert $ x_{sp} $ to Single Cosine form.
Amplitude $ C = \sqrt{5^2 + 4^2} = \sqrt{41} \approx 6.403 $.
Phase Angle $ \alpha = \arctan(4/5) \approx 0.6747 $ radians.
Result: $ x_{sp}(t) = \sqrt{41} \cos(4t - 0.6747) $.

Step 4: Solve the Initial Value Problem for $ C_1 $ and $ C_2 $.
The general solution is $ x(t) = e^{-t}(C_1 \cos(5t) + C_2 \sin(5t)) + 5 \cos(4t) + 4 \sin(4t) $.
Using the initial position $ x(0) = 6 $: $$x(0) = C_1 + 5 = 6 \implies C_1 = 1$$ Differentiating the general solution: $$x'(t) = -e^{-t}(C_1 \cos 5t + C_2 \sin 5t) + e^{-t}(-5C_1 \sin 5t + 5C_2 \cos 5t) - 20 \sin 4t + 16 \cos 4t$$ Using the initial velocity $ x'(0) = 0 $: $$x'(0) = -C_1 + 5C_2 + 16 = 0 \implies -1 + 5C_2 + 16 = 0 \implies 5C_2 = -15 \implies C_2 = -3$$

Final Particular Solution: $$x(t) = e^{-t}(\cos(5t) - 3 \sin(5t)) + 5 \cos(4t) + 4 \sin(4t)$$ Transient Solution:$$x_{tr}(t) = e^{-t}(\cos(5t)-3\sin(5t))$$ Steady-Periodic Solution: $$ x_{sp}(t) = \sqrt{41} \cos(4t - 0.6747) $$

Step 5: Practical Resonance Investigation.
Practical resonance occurs when the steady-state amplitude $ C(\omega) $ is maximized. For this system: $$C(\omega) = \frac{82}{\sqrt{(26 - \omega^2)^2 + (2\omega)^2}}$$ The amplitude is maximized when the term inside the square root is minimized:
Let $ f(\omega^2) = (26 - \omega^2)^2 + 4\omega^2 = 676 - 52\omega^2 + \omega^4 + 4\omega^2 = \omega^4 - 48\omega^2 + 676 $.
Completing the square: $ f(\omega^2) = (\omega^2 - 24)^2 + 100 $.
The minimum occurs when $ \omega^2 = 24 $. Thus, practical resonance occurs at frequency: $$\omega = \sqrt{24} = 2\sqrt{6} \approx 4.899 \text{ radians per second}$$

Lecture 20 & 21 Section 3.6