(I) Separation of Variables
Consider the 1st order D.E. \(\frac{dy}{dx} = f(x, y)\). This equation is called separable if it can be written as:
The method involves moving all terms containing \(y\) to one side and all terms containing \(x\) to the other, then integrating: \(\int h(y) \, dy = \int g(x) \, dx\).
(1) Solve \((1+x)\frac{dy}{dx} = 4y\):
\(\int \frac{1}{y} \, dy = \int \frac{4}{1+x} \, dx \implies \ln|y| = 4\ln|1+x| + C_1\)
\(|y| = e^{4\ln|1+x| + C_1} = e^{C_1}|1+x|^4\)
General solution: \(y = C(1+x)^4\)
(2) If \(y(0) = 5\), solve the I.V.P.:
\(y(0) = C(1+0)^4 = 5 \implies C = 5 \implies y = 5(1+x)^4\)
Solve the I.V.P.: \(\frac{dy}{dx} = \frac{4-2x}{3y^2-5}, \quad y(1) = 3\)
Note that \(3y^2 - 5 \neq 0\). The slope becomes infinite as \(y \to \pm\sqrt{5/3} \approx \pm 1.29\).
\(\int (3y^2-5) \, dy = \int (4-2x) \, dx \implies y^3 - 5y = 4x - x^2 + C\)
Using \(y(1)=3\): \(3^3 - 5(3) = 4(1) - 1^2 + C \implies 12 = 3 + C \implies C = 9\).
Implicit particular solution: \(y^3 - 5y + x^2 - 4x = 9\).
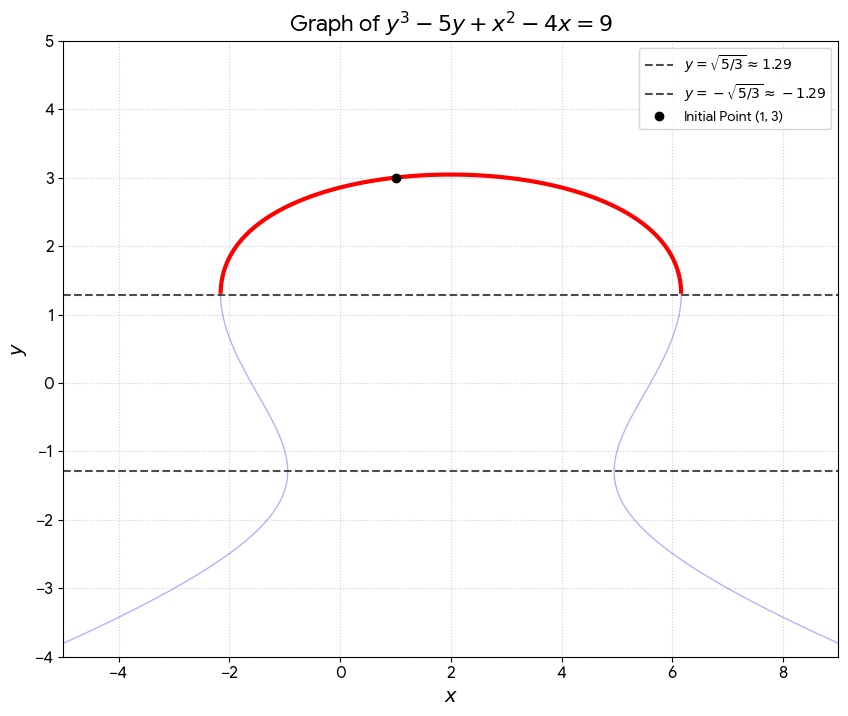
The solution curve for the I.V.P. is the portion that avoids the lines \(y = \pm\sqrt{5/3}\).
(II) General, Implicit, and Singular Solutions
- Implicit Solution: A relation \(K(x, y) = 0\) satisfied by a solution \(y(x)\).
- General Solution: Contains an arbitrary constant \(C\). Specific values yield particular solutions.
- Singular Solution: An exceptional solution that cannot be obtained from the general solution by choosing \(C\).
Find ALL solutions of \(\frac{dy}{dx} = 6x(y-1)^{2/3}\).
If \(y \neq 1\), integrating gives: \(\int \frac{1}{3(y-1)^{2/3}} \, dy = \int 2x \, dx \implies (y-1)^{1/3} = x^2 + C\).
General solution: \(y(x) = (x^2 + C)^3 + 1\).
However, \(y(x) \equiv 1\) also satisfies the D.E. Since it cannot be produced by choice of \(C\), \(y = 1\) is a singular solution.
(III) Natural Growth and Decay
The solution to \(\frac{dX}{dt} = kX\) is:
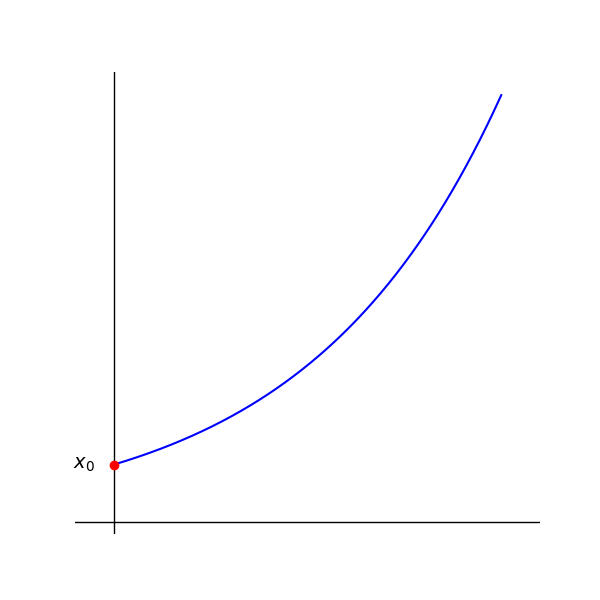
Natural Growth (\(k > 0\))
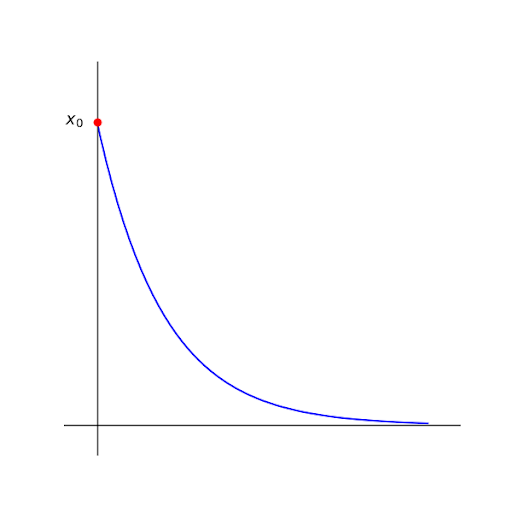
Natural Decay (\(k < 0\))
Key Applications:
- Population Growth: Modeled where \(k\) is net increase.
- Drug Elimination: Rate a substance leaves the bloodstream.
- Radioactive Decay:
Consider a sample that contains \(N(t)\) atoms of a radioactive isotope at time \(t\). The rate of change is proportional to the amount present
The solution is \(N(t) = N_0 e^{-kt}\). The decay constant \(k\) is often specified in terms of the half-life (\(\tau\)): \(\tau = \frac{\ln 2}{k}\). \(\tau\) is the time required for half of the isotope to decay. For example, the half-life of \(^{14}C\) is approximately 5700 years.
(IV) Cooling and Heating
Newton's Law of Cooling: \(\frac{dT}{dt} = k(A - T)\).
Problem: A roast initially at \(50^\circ F\) is placed in a \(375^\circ F\) oven at 5:00 pm. After 75 minutes, its temperature is \(125^\circ F\). When will it be \(150^\circ F\)?
Differential Equation Setup: $$\frac{dT}{dt} = k(375 - T), \quad T(0) = 50, \quad T(75) = 125$$
1. Separation: \(\int \frac{1}{375 - T} \, dT = \int k \, dt \implies -\ln|375 - T| = kt + C_1\).
2. General Solution:
Multiply by \(-1\): \(\ln|375 - T| = -kt - C_1\).
Exponentiate: \(|375 - T| = e^{-kt - C_1} = e^{-C_1}e^{-kt}\).
Let \(C = \pm e^{-C_1}\): \(375 - T = Ce^{-kt} \implies T(t) = 375 - Ce^{-kt}\).
3. Initial Condition \(T(0) = 50\): \(50 = 375 - C(1) \implies C = 325 \implies T(t) = 375 - 325e^{-kt}\).
4. Solving for \(k\) using \(T(75) = 125\):
\(125 = 375 - 325e^{-75k} \implies 325e^{-75k} = 250\)
\(e^{-75k} = \frac{250}{325} \implies -75k = \ln\left(\frac{10}{13}\right) \implies k \approx 0.0035\).
5. Finding Time for \(T = 150\):
\(150 = 375 - 325e^{-0.0035t} \implies 325e^{-0.0035t} = 225\)
\(e^{-0.0035t} = \frac{225}{325} \implies -0.0035t = \ln\left(\frac{9}{13}\right) \implies t \approx 105 \text{ min}\).
Conclusion: 105 minutes after 5:00 pm is 6:45 pm.