MATLAB Educational Demos

Orbital Mechanics

space_debris_simulation.m

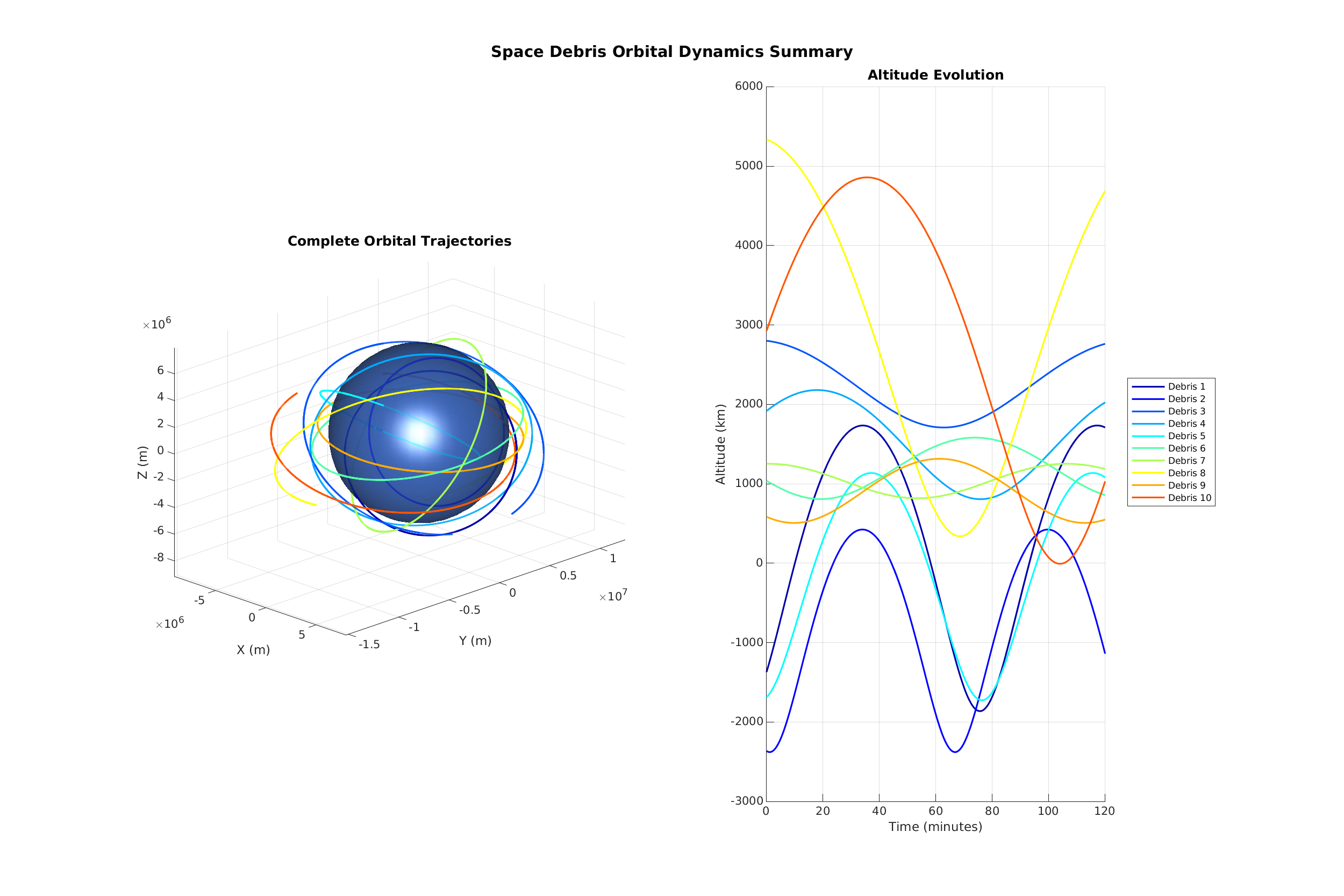
Simulates orbital dynamics of 10 debris objects around Earth under gravitational force. Random initial conditions with varying altitudes (300–2000 km), inclinations, and eccentricities.

Method: Numerical integration of Newton's equations in 3D. 2-hour simulation, 10s time step.

Satellite Tracking

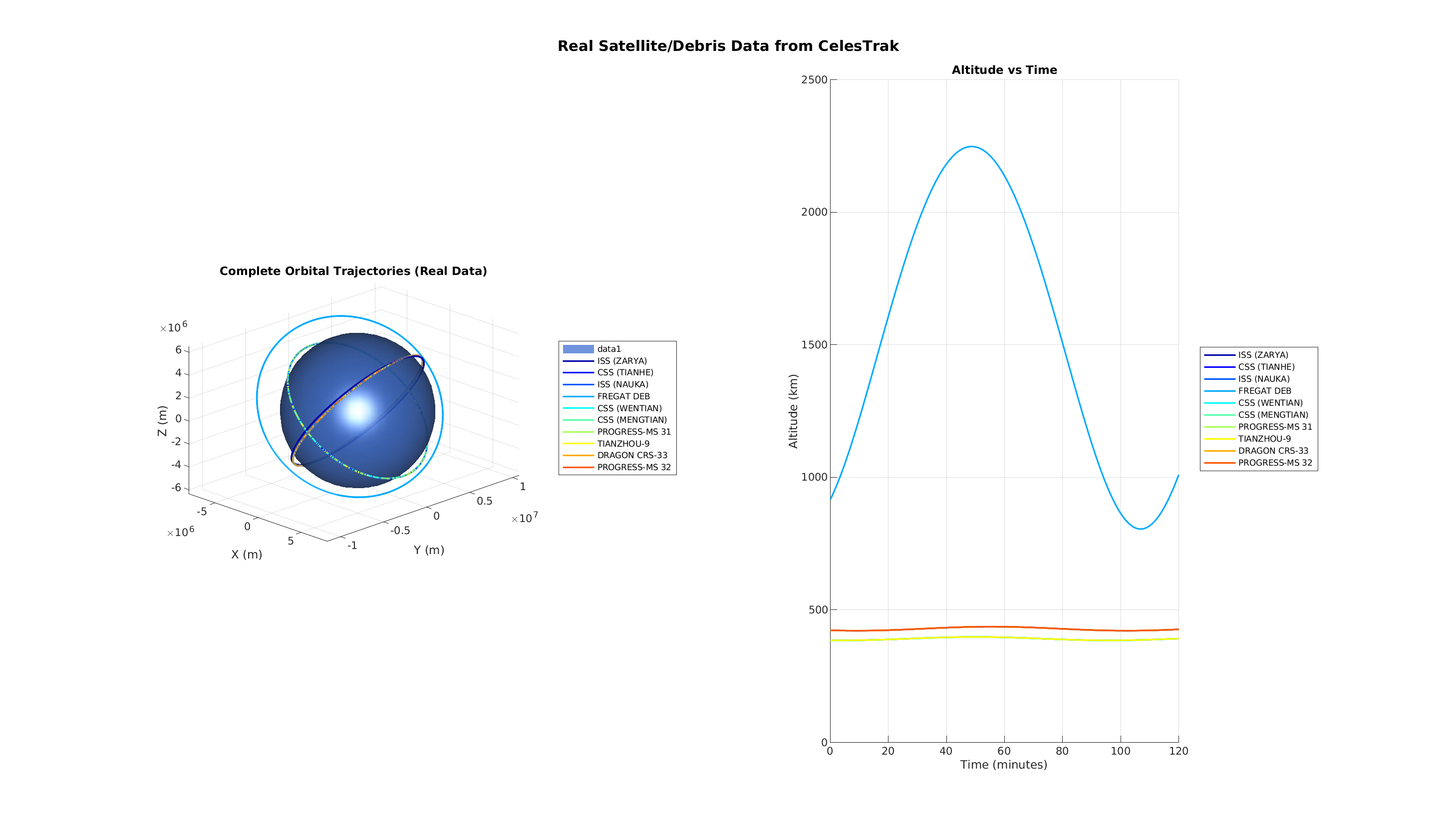
space_debris_real_data.m

Loads real satellite orbital data from TLE (Two-Line Element) format files and propagates orbits using Keplerian elements. 3D visualization of real satellite orbits.

Dataset: iss_tle_data.txt (source: CelesTrak).

Large-Scale Satellites

space_debris_large_dataset.m

Processes and visualizes a large TLE dataset (~14,000+ active satellites). Subsamples 50 for animation and 200 for full trajectory output suitable for operator learning.

Dataset: active_satellites_full.txt (source: CelesTrak active satellites catalog). 2-hour simulation, 15s time step.

Central Limit Theorem

galton_board.m

Simulates balls dropping through a Galton board (peg board) into bins, demonstrating that the resulting distribution approximates a Gaussian. A theoretical normal curve is overlaid on the histogram.

Random Walk (Sphere)

rw_pointcloud.m

Generates 800 uniform points on a unit sphere (Fibonacci spiral), builds a k=10 nearest-neighbor graph, simulates a 5000-step random walk. Stationary distribution is approximately uniform.

Transition rule: Uniform random choice among k nearest neighbors.

Random Walk (Bunny)

rw_bunny.m

Loads Stanford Bunny mesh (8171 vertices), subsamples to 1500 points, builds k=12 nearest-neighbor graph, simulates an 8000-step random walk. Non-uniform density produces a non-uniform stationary distribution.

Dataset: bunny.ply (source: Stanford 3D Scanning Repository).

2D Acoustic Wave Equation

acoustic_wave_2d.m

Simulates wave propagation on a 10×10 m domain with a circular rigid obstacle. A Gaussian pulse is launched from the left side and scatters off the obstacle.

Method: Second-order finite differences in space, leap-frog in time. Dirichlet BCs. 300×300 grid.

Heterogeneous Wave

acoustic_wave_2d_heterogeneous.m

Extends the acoustic wave demo to spatially varying wave speed c(x,y). The medium has horizontal layers, random heterogeneity, and a high-speed lens that focuses waves.

Method: Variable-coefficient wave equation with gradient terms. First-order Mur absorbing BCs. 400×400 grid.

Shock Capturing / CFD

lax_friedrichs_shock_tube.m

Solves the 1D compressible Euler equations for the Lax shock tube problem. Produces a rarefaction wave, contact discontinuity, and shock wave from discontinuous initial data.

Method: First-order Lax-Friedrichs scheme, CFL=0.9. 200 points on [0, 1], final time T=0.14.

Compressed Sensing

douglas_rachford_basis_pursuit.m

Solves basis pursuit (minimize ‖x‖₁ subject to Ax = b) using Douglas-Rachford splitting. Recovers a sparse signal (20 nonzero entries in 1000 dimensions) from 100 measurements.

Method: Douglas-Rachford iteration alternating between affine projection and soft thresholding.

Optimal Transport

optimal_transport_1d.m

Computes and animates optimal transport between two 1D Gaussians using the Benamou-Brenier dynamical formulation. Source: narrow Gaussian at x=−1.5. Target: wider Gaussian at x=1.5.

Method: CDF inversion for the optimal map T(x) = F₁⁻¹(F₀(x)). McCann interpolation for the Wasserstein geodesic.

Optimal Transport (Merge)

optimal_transport_1d_merge.m

Transports a bimodal distribution (two Gaussians at x=−2 and x=2) to a single Gaussian at the origin. Demonstrates how mass from two sources optimally merges into one.

Method: Same CDF-based approach. Animation shows two bumps flowing inward and merging.

MCMC / Langevin Dynamics

langevin_mcmc.m

Demonstrates Langevin dynamics for sampling from a Gibbs distribution using Euler-Maruyama discretization of the Langevin SDE with a double-well potential U(x) = (x²−1)².

Animation: Particle on potential landscape, sample path over time, histogram converging to the Gibbs distribution.

MALA

mala_mcmc.m

Extends Langevin MCMC by adding a Metropolis-Hastings accept/reject step to the Langevin proposal, correcting for discretization bias.

Animation: 4 panels including running acceptance rate plot.

ULA vs MALA Comparison

compare_ula_mala.m

Runs both Unadjusted Langevin (ULA) and MALA side-by-side with the same noise sequence, comparing convergence to the Gibbs distribution via KL divergence.

Animation: Side-by-side histograms, KL divergence on semilogy scale.

CNN Regression

cnn_regression.m

Trains a CNN to fit a smooth function f(x) = sin(2x) + 0.5cos(5x) + 0.3sin(8x). Uses Gabor-like patch encoding to convert 1D input to 2D image patches.

Optimizer: Adam. Animation shows fitted curve evolving during training.

CNN Classification

cnn_classification.m

Trains a CNN to classify a 4-class spiral dataset in 2D. Uses 2D patch encoding and shows decision boundary evolution during training.

Concepts: Cross-entropy loss, softmax, decision boundaries, training/validation split.

Optimizer Comparison

cnn_regression_optimizers.m

Compares 7 optimization methods on the same CNN regression problem: Vanilla GD, SGD, Heavy Ball Momentum, Nesterov, AdaGrad, RMSProp, and Adam. All implemented from scratch with custom training loops.

Animation: 7 fitted curves side-by-side with MSE loss comparison.

Autoencoder

autoencoder_pointcloud.m

Trains an autoencoder (150→128→64→32→2→32→64→128→150) to compress 3D point clouds of 5 shape classes into a 2D latent space. Compares to PCA.

Key insight: Random point ordering makes reconstruction impossible — fixed by deterministic ordered sampling.

AE vs PCA

autoencoder_curved_boundary.m

Designed to show where autoencoders beat PCA. Data lives on a nonlinear manifold (2D latent mapped to 50D via sinusoidal features). Three classes with concentric circular boundaries.

Result: AE achieves ~84% KNN accuracy vs PCA's ~72%.

Tabular RL

rl_gridworld.m

Solves an 8×8 grid world (obstacles, traps, goal) using exact policy iteration: alternating policy evaluation (Bellman equation) and greedy policy improvement.

Animation: Value function heatmap and policy arrows evolving, then agent following the optimal path.

Deep Q-Network

rl_gridworld_dqn.m

Same grid world, but Q(s,a) is approximated by a neural network (7→64→64→4) trained with Adam and experience replay. Compares learned DQN policy to exact tabular solution.

Result: ~60% policy match vs tabular optimal after 800 episodes.

Mean Field Games

mean_field_game_demo.m

Solves a 1D Mean Field Game for crowd congestion. Agents on [0,1] move toward a target while avoiding congested areas, subject to Brownian noise. The equilibrium balances proximity-to-target against congestion cost.

Method: Fictitious play iterating between HJB backward sweep (Godunov Hamiltonian) and Fokker-Planck forward sweep (upwind advection). Converges in ~27 iterations.

Poisson Convergence

poisson2d_convergence.m

Solves −Δu = f on [0,1]×[0,1] with Dirichlet BCs using second-order finite differences. Manufactured solution u(x,y) = sin(2πx)sin(2πy) provides an exact reference.

Method: 2D Laplacian via Kronecker products. Tests N = 16, 32, 64. Expected: 2nd-order convergence.

Discontinuous Galerkin

dg_euler_2d_positivity.m

Solves the 2D compressible Euler equations using a Q2 Discontinuous Galerkin method with the Zhang-Shu positivity-preserving limiter on a circular explosion benchmark.

Method: Q2 DG, 9 basis functions/element, Gauss-Legendre quadrature. 30×30 elements.

DG Convergence Study

dg_euler_2d_accuracy_test.m

Measures accuracy and convergence rate of the Q2 DG Euler solver using the isentropic vortex benchmark. Tests multiple mesh resolutions and computes L2 errors.

Expected: ~3rd order convergence for Q2 elements on periodic domain.