Euler characteristic and genus
We now want to give the precise definition of genus. We can start with the famous
formula of Euler. Given a polyhedron
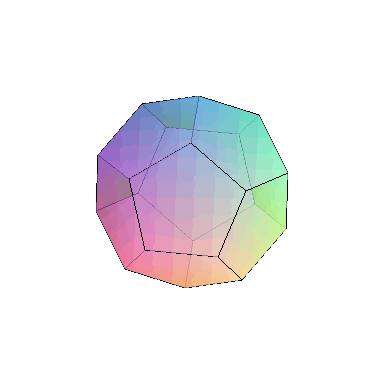 with V vertices, E edges and F faces
with V vertices, E edges and F faces
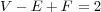 The
unstated assumption is that the surface of the polyhedron is homeomorphic to the
sphere. However, we can form polyhedra homeomorphic to other surfaces. The
following is homeomorphic to a torus,
The
unstated assumption is that the surface of the polyhedron is homeomorphic to the
sphere. However, we can form polyhedra homeomorphic to other surfaces. The
following is homeomorphic to a torus,
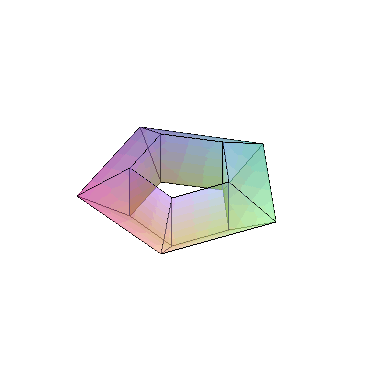 In such cases, we get
In such cases, we get
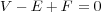 The
point is that this expression called the Euler characteristic χ depends only on the
surface. If S is compact oriented surface (e.g. a complex curves with points of
infinity included) then χ(S) is known to even, and the genus g can be defined
by
The
point is that this expression called the Euler characteristic χ depends only on the
surface. If S is compact oriented surface (e.g. a complex curves with points of
infinity included) then χ(S) is known to even, and the genus g can be defined
by
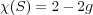 The
genus can be understood intuitively as the “number of holes”. For example, a genus
two surface or “two holed doughnut” is depicted below.
The
genus can be understood intuitively as the “number of holes”. For example, a genus
two surface or “two holed doughnut” is depicted below.
 Consider the hyperelliptic curve X defined by an equation y2 = p(x) where p(x) has an odd degree, say n, with distinct roots.
We give a formula (due to Riemann and Hurwitz) for the
genus g of X.
We triangulate C ∪{∞} so that the roots of p(x) and ∞ are included
among the vertices. Let’s say that there are V verticies, E edges and F faces. So that
V - E + F = 2. The preimage of this triangulation gives a triangulation of X
with V ′ vertices etcetera. We have V ′- E′ + F′ = 2 - 2g. The map from X → C ∪{∞} is two to one except at vertices
lying over the roots and ∞ where it one to one. Thus V ′ = 2V - n - 1, E′ = 2E, F′ = 2F, so
that
Consider the hyperelliptic curve X defined by an equation y2 = p(x) where p(x) has an odd degree, say n, with distinct roots.
We give a formula (due to Riemann and Hurwitz) for the
genus g of X.
We triangulate C ∪{∞} so that the roots of p(x) and ∞ are included
among the vertices. Let’s say that there are V verticies, E edges and F faces. So that
V - E + F = 2. The preimage of this triangulation gives a triangulation of X
with V ′ vertices etcetera. We have V ′- E′ + F′ = 2 - 2g. The map from X → C ∪{∞} is two to one except at vertices
lying over the roots and ∞ where it one to one. Thus V ′ = 2V - n - 1, E′ = 2E, F′ = 2F, so
that
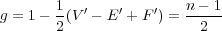
Although the definition is topological, it turns out that the genus is strongly
connected to the complex function theory of a curve. The relationship is given by the
Riemann-Roch theorem. We will explain a special case. First observe that a
holomorphic function on a compact connected complex curve X is necessarily
constant.
Proof: Since X is compact, the modulus of the function must attain a maximum
at some point p. By the maximum modulus principle the function must be constant
in a neighbourhood of p. This implies that f = f(p) everywhere since the difference
has nonisolated zero.
Therefore nonconstant meromorphic functions on X must have singularities.
Which raises the question, what are simplest possible singularities? Choose
points p1,…pk  X and positive integers n1,…nk. Then the Riemann-Roch theorem
tells us that there is a nonconstant function with poles only at pi of order at most ni,
provided that n1 + … + nk > g. A standard proof uses a refined form
of the Euler characteristic.
X and positive integers n1,…nk. Then the Riemann-Roch theorem
tells us that there is a nonconstant function with poles only at pi of order at most ni,
provided that n1 + … + nk > g. A standard proof uses a refined form
of the Euler characteristic.
Return to first page.
Go to next page.
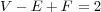
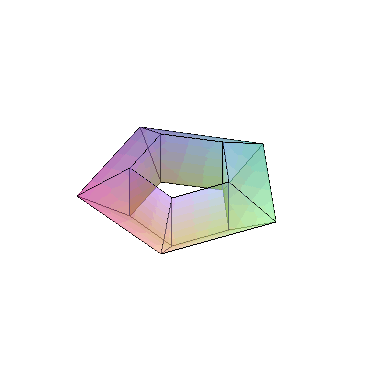
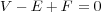
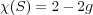

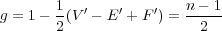
 X and positive integers n1,…nk. Then the Riemann-Roch theorem
tells us that there is a nonconstant function with poles only at pi of order at most ni,
provided that n1 + … + nk > g. A standard proof uses a refined form
of the Euler characteristic.
X and positive integers n1,…nk. Then the Riemann-Roch theorem
tells us that there is a nonconstant function with poles only at pi of order at most ni,
provided that n1 + … + nk > g. A standard proof uses a refined form
of the Euler characteristic.