Automorphic functions and Uniformization

The line C ∪{∞} is topologically just a sphere, which is positively curved. (The precise definition of Gaussian curvature Kcan be found in any basic differential geometry text.) We were able to parameterize an elliptic curve by using elliptic functions on the complex plane. These were periodic with respect to a tiling of the plane by parallelograms. This shows that elliptic curve can be given a metric which is flat i.e. has zero curvature. For a compact surface X with genus g ≥ 2, the Gauss-Bonnet theorem that says the total curvature

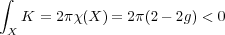
∫ K = 2π χ(X) = 2π(2 - 2g) < 0 X

In fact the uniformation theorem tells us that we can choose a metric with constant negative curvature in this case. This means that the relevant geometry here is hyperbolic. There are two equivalent basic models: the upper half plane

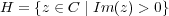
H = {z ∈ C | Im(z) > 0}

and the disk

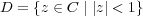
D = {z ∈ C | |z| < 1}

We can map H onto D by

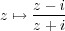
z ↦→ z --i z + i

We give these the Poincaré metric where geodisics (“straight lines”) are circles meeting the real line or unit circle at right angles. X can be then be realized as a a quotient of H (or D) by a group Γ. We can think of Γ (roughly) as the group of symmetries of a hyperbolic tiling Graph

The function theory of X can the be studied in terms of functions on H (or D) invariant or almost invariant under Γ. Such functions are called automorphic. The basic example of an automorphic function on H is the modular j function, given by the Fourier series

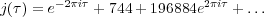
j(τ) = e-2πiτ + 744+ 196884e2πiτ + ...

This function comes up naturally in the theory of elliptic curves. The elliptic curves determined by the lattices {m + nτ∣m,n

Z} and {m + nτ′∣m,n

Z} are isomorphic if and only if j(τ) = j(τ′). This is a nonconstant meromorphic function on H satisfying

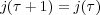
j(τ + 1) = j(τ)

1 j(---) = j(τ) τ

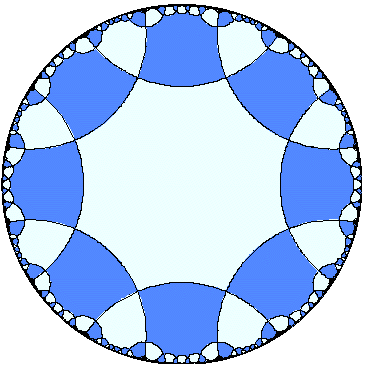
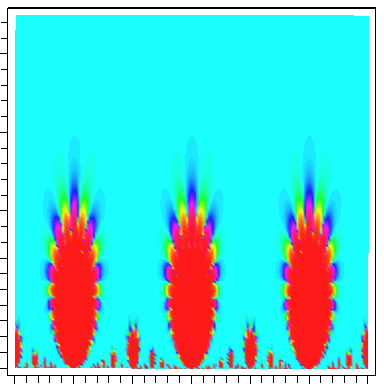
In other words j is invariant under the group generated by translations τ → τ + 1 and the inversion τ →-1∕τ (which is abstractly PSL₂(Z)). Here we give a graph of j , where these symmetries are in evidence (colours corresponds to values of Re(j(τ)) with red corresponding to larger values).

Return to first page. Go to next page.