\begin{equation*} \def\P{\mathcal{P}} \def\A{\mathcal{A}} \def\B{\mathcal{B}} \def\F{\mathbb{F}} \def\R{\mathbb{R}} \def\C{\mathbb{C}} \def\Q{\mathbb{Q}} \def\od{\stackrel{\mathrm{def}}{=}} \def\U{\mathcal{U}} \def\rr{\mathcal{R}} \def\Z{\mathbb{Z}} \def\N{\mathbb{N}} \def\H{\mathbb{H}} \def\p{\mathfrak{p}} \def\q{\mathfrak{q}} \def\m{\mathfrak{m}} \def\n{\mathfrak{n}} \def\supp{\operatorname{supp}} \def\geom{\operatorname{geom}} \def\det{\operatorname{det}} \def\ker{\mathop{\rm ker}} \def\coker{\mathop{\rm coker}} \def\im{\mathop{\rm im}} \def\id{\mathop{\rm id}} \def\hom{\mathop{\rm Hom}} \def\soc{\mathop{\rm Soc}} \def\rad{\mathop{\rm Rad}} \def\nil{\mathop{\rm nil}} \def\aut{\mathop{\rm Aut}} \def\quot{\mathop{\rm Quot}} \def\spec{\mathop{\rm Spec}} \def\dep{\mathop{\rm Depth}} \def\grd{\mathop{\rm grade}} \def\trdg{\mathop{\rm Trdg}} \def\spt{\mathop{\rm Supp}} \def\sup{\mathop{\rm sup}} \def\sym{\mathop{\rm Sym}} \def\gr{\mathop{\rm gr}} \def\chr{\mathop{\rm char}} \def\mspec{\mathop{\rm m-Spec}} \def\ass{\mathop{\rm Ass}} \def\ann{\mathop{\rm ann}} \def\dim{\mathop{\rm dim}} \def\tor{\mathop{\rm Tor}} \def\ext{\mathop{\rm Ext}} \def\projdim{\mathop{\rm projdim}} \def\injdim{\mathop{\rm injdim}} \def\hgt{\mathop{\rm ht}} \def\mod{\mathop{\rm mod}} \def\rank{\mathop{\rm rank}} \def\max{\mathop{\rm max}} \newcommand\colim{\mathop{\mathrm{colim}}\nolimits} \newcommand\lim{\mathop{\mathrm{lim}}\nolimits} \newcommand\Qcoh{\mathit{Qcoh}} \newcommand\Sch{\mathit{Sch}} \newcommand\QCohstack{\mathcal{QC}\!\mathit{oh}} \newcommand\Cohstack{\mathcal{C}\!\mathit{oh}} \newcommand\Spacesstack{\mathcal{S}\!\mathit{paces}} \newcommand\Quotfunctor{\mathrm{Quot}} \newcommand\Hilbfunctor{\mathrm{Hilb}} \newcommand\Curvesstack{\mathcal{C}\!\mathit{urves}} \newcommand\Polarizedstack{\mathcal{P}\!\mathit{olarized}} \newcommand\Complexesstack{\mathcal{C}\!\mathit{omplexes}} \newcommand\Pic{\mathop{\mathrm{Pic}}\nolimits} \newcommand\Picardstack{\mathcal{P}\!\mathit{ic}} \newcommand\Picardfunctor{\mathrm{Pic}} \newcommand\Deformationcategory{\mathcal{D}\!\mathit{ef}} \end{equation*}
  1. People

Pythagorean Triples

Certainly anybody that has passed grade school math has at least heard of the Pythagorean theorem. It is of course the iconic formula which relates the side lengths of a right triangle:

$$a^2+b^2=c^2$$

Without too much difficulty, one can find some postive integer solutions to this, $3^2+4^2=5^2$, $5^2+12^2=13^2$, etc. Whereas the existence of integer solutions is uninteresting, a better question to ask is how many triples $(a,b,c)$ of integers satisfying the equation actually exist.

However, there are some rules we should impose first. Naturally, given a triple we can generate infinitely many more simply by scaling by an integer constant. For example certainly $(3,4,5)$ is a Pythagorean triple as $3^2+4^2=5^2$ so then $(3c)^2+(4c)^2=(5c)^2$ is also a Pythagorean triple for any integer $c$, but somehow we should associate this triple with the first since this is really nothing new. To avoid something like this we say we wish to find all classes of Pythagorean triples $(a:b:c)$ where the colons represent the abscence of any common factors between the three terms. To do this, let us produce some type of invariant that distinguishes between each class of solution. Consider the fraction:

$$\frac{a}{c-b}$$

Certainly if there is a common factor that divides $a$ , $b$, and $c$ it will cancel out in the fraction and so we claim that this quantity is unique to each class. Notice that

$$\frac{a}{c-b} = \frac{a}{c-b}\cdot\frac{c+b}{c+b} = \frac{a(c+b)}{c^2-b^2} = \frac{a(c+b)}{a^2} = \frac{c+b}{a}$$

and so we have two different ways to view this ratio, but now let us introduce a third. As there could be the possibility of cancellations of some common factors between $a$ and the sum/difference, let $s$ and $t$ be integers so that

$$\frac{s}{t} = \frac{a}{c-b}=\frac{c+b}{a}$$ Now that we have this reduced fraction, let us homogenize and proceed in a geometric fashion. $$a^2+b^2=c^2 \Longrightarrow \bigg(\frac{a}{c}\bigg)^2+\bigg(\frac{b}{c}\bigg)^2=1$$

Let $x=\frac{a}{c}$ and $y=\frac{b}{c}$ and now notice that finding integer solutions $(a:b:c)$ is now equivalent to finding rational solutions $(x:y:1)$. Also note that

$$\frac{s}{t} = \frac{b+c}{a} = \frac{b/c+c/c}{a/c} = \frac{y+1}{x}$$ Hence we have a system of equations we are looking to satisfy: \[ \left\{ \begin{array}{l} x^2+y^2=1\\ y=\frac{s}{t}x-1 \end{array} \right. \]

Geometrically this solution is just the intersection between the line of slope $\frac{s}{t}$ passing through $(0,-1)$ with the unit circle.

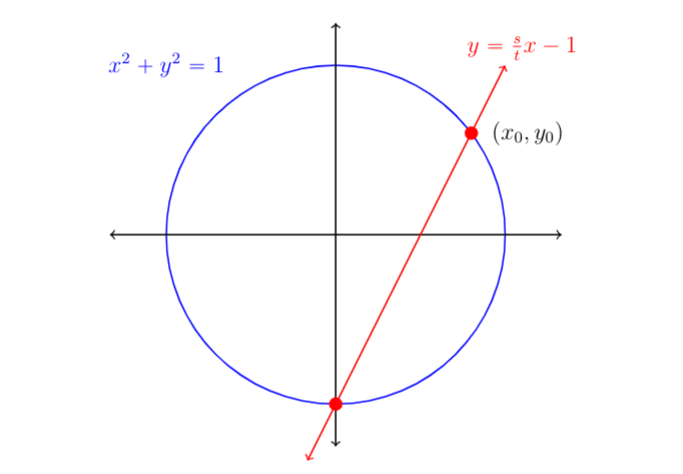
Thus for any rational class of solutions $(x:y:1)$ and hence integer class $(a:b:c)$, the set of solutions is completely determined by the slope of this line. Hence any class of solutions is equivalent if and only if they have the same values for $s$ and $t$ (as $s$ and $t$ are assumed to be coprime). With this in mind let us use this now unique fraction to generate all solutions. Let us first figure what this solution above is. Substituting to solve the system of equations,

\begin{align*} x^2 + \bigg(\frac{s}{t}x-1\bigg)^2=&1\\[1ex] x^2+ \bigg( \frac{s^2}{t^2}x^2 -\frac{2s}{t}x+1\bigg) =&1\\[1ex] \bigg( 1+\frac{s^2}{t^2}\bigg)x^2 - \frac{2s}{t}x=&0\\[1ex] x\bigg(\bigg( 1+\frac{s^2}{t^2}\bigg)x- \frac{2s}{t}\bigg)=&0\\[1ex] \end{align*} Now $x=0$ gives us the $y$-intercept point which was already known and so this leads to the trivial solution $1^2+0^2=1^2$. Then the nontrivial solution occurs when the other term is zero, i.e. $$ \bigg( 1+\frac{s^2}{t^2}\bigg)x =\bigg( \frac{s^2+t^2}{t^2}\bigg)x = \frac{2s}{t} $$ Then $$x= \frac{2s}{t} \cdot\frac{t^2}{s^2+t^2} = \boxed{\frac{2st}{s^2+t^2}}$$ Now solving for $y$ $$ y =\frac{s}{t}\cdot \frac{2st}{s^2+t^2} -1 =\frac{2s^2-(s^2+t^2)}{s^2+t^2} = \boxed{ \frac{s^2-t^2}{s^2+t^2} }$$ Thus $$(x:y:1) = \bigg( \frac{2st}{s^2+t^2} \hspace{1mm}:\hspace{1mm}\frac{s^2-t^2}{s^2+t^2} \hspace{1mm}:\hspace{1mm}1\bigg)$$ Returning to the original task: $$(a:b:c) = \boxed{\big(2st \hspace{1mm}:\hspace{1mm}s^2-t^2\hspace{1mm}:\hspace{1mm}s^2+t^2\big)}$$

Now in order to generate a nontrivial Pythagorean triple, all one needs to do is choose coprime integers $s$ and $t$ (as the fraction $\frac{s}{t}$ was taken to be reduced). Now as there are infinitely choices for $s$ and $t$, we conclude that there are infinitely many distinct Pythagorean triples and they are all of this form.

For example, let $s=28$ and $t =15$. Then
  • $a= 2(28)(15) = 840$
  • $b =28^2-15^2 = 559$
  • $c= 28^2+15^2 = 1009$
One easily checks and confirms that $$840^2+559^2=1009^2$$ And so indeed, we have show that there exist infinitely many distinct classes of Pythagorean triples and moreover, we have produced a method to generate them.