Placement and ALEKS Learning Module Information
IMPORTANT NOTICE:
ALEKS Placement Assessment now requires LockDown Browser and Respondus Monitor
- Placing into a mathematics course
- Scores required for placement
- Who should take the ALEKS Placement Assessment?
- What if I'm not sure I need to take ALEKS?
- How do I begin using ALEKS?
- Is there a fee for using ALEKS?
- Can I retake the ALEKS Placement Assessment?
- Are ALEKS Placement Assessments proctored?
- May I use a calculator while using ALEKS?
- May I use any other resources during a placement assessment?
- Can I retake the ALEKS Placement Assessment immediately?
- Must I work in my ALEKS Prep and Learning Module between placement assessments?
- Are placement assessments timed?
- How long will a placement assessment take to complete?
- What is my placement result?
- Can I practice using ALEKS before I begin placement?
- How long do I have access to my Prep and Learning Module?
- What are ALEKS Progress Assessments?
- Does progress in an ALEKS Prep and Learning Module count toward placement?
- Which Prep and Learning Moduel should I choose?
- Can I change to a different Prep and Learning Module later?
- What if I do not place into the course I wanted?
- I did not place into the class I wanted. Can I take it anyway?
- What if I placed into the class I wanted?
- Where can I get help with ALEKS?
- What about Advanced Placement (AP) credit?
- What is the deadline for taking ALEKS?
- Problems taking ALEKS?
Placing into a mathematics course
Students who have established credit for a Purdue math class (via AP, IB, transfer, or dual credit) are typically placed into an appropriate math class in their first semester based on that credit.
Students who have not established credit are placed into a Purdue math class based on SAT Math, ACT Math, or ALEKS mathematics placement assessment scores according to the following guidelines:
- If you have an SAT Math score of at least 670 or an ACT Math score of at least 29, then you do NOT need to take ALEKS in order to register for a math class for the upcoming semester.
- If you have neither an SAT Math score of at least 530 nor an ACT Math score of at least 21, then you must obtain an ALEKS score of at least 45% before you can register for a math class for the upcoming semester. (This is also true of students who do not have an SAT/ACT score.)
- If you have an SAT Math score in the range 530 to 660 OR an ACT Math score in the range 21 to 28, then please examine the table below to determine IF you must take ALEKS in order to register for your desired math class at Purdue.
Students may place into the classes shown in the table below in one of three ways: with a suitable score on the math component of either the SAT or ACT or with a suitable score on the ALEKS Placement Assessment. (See the documentation below for more information about ALEKS.) Because math requirements vary greatly among majors and colleges, students are encouraged to consult the University course catalog and look at the plans of study they are considering to determine which initial math class they should take. Individuals who have further questions may contact their college’s advising office.
Remember only one of the three scores is required to place into the course. You can use an ALEKS score for placement even with a lower SAT or ACT Math score. If you need to take ALEKS and are planning to register for classes during All-Aboard, then you should complete ALEKS prior to attending your Purdue 101 advising appointment.
Scores required for placement
|
Course |
Description |
SAT |
ACT |
ALEKS |
SAT |
|---|---|---|---|---|---|
|
MA 13700 |
Mathematics For Elementary Teachers I |
530 |
21 |
45 |
500 |
|
MA 15300 |
Algebra And Trigonometry I |
530 |
21 |
45 |
500 |
|
MA 15555 |
Quantitative Reasoning |
530 |
21 |
45 |
500 |
|
MA 15800 |
Precalculus |
570 |
24 |
60 |
550 |
|
MA 16010 |
Applied Calculus I |
620 |
26 |
75 |
600 |
|
MA 16100 |
Plane Analytic Geometry And Calculus I |
670 |
29 |
85 |
650 |
Who should take the ALEKS Placement Assessment?
The ALEKS Placement Assessment covers material from basic mathematics through precalculus and will take approximately 90 minutes to complete.
If you already have an SAT Math or ACT Math score that meets or exceeds course requirements listed above you do not have to take the ALEKS Placement Assessment to place into a mathematics course.
Even if you place into your desired mathematics course with your SAT or ACT scores, all students are able to take the ALEKS Placement Assessment and use the learning modules. There is no penalty for taking an ALEKS assessment as you can use your qualifying score in either ALEKS, SAT Math, or ACT Math for placement.
It is important that you relax and that you are honest about your skill level. Therefore, while you are taking the assessment, do not consult any other source for help. Remember, you not only want to get into the right course, you want to be very successful in that course. This is simply an assessment, not a test. The difference is that an assessment is designed to determine what you know in order to best serve your academic success at Purdue University.
At the end of the ALEKS Placement Assessment, you will have a much better sense of your strengths and weaknesses in math. You will then have a chance to work on those weaknesses through a targeted Prep and Learning Module geared to your goals to improve placement and eventual course outcomes.
What if I'm not sure I need to take ALEKS?
Take it anyway! It’s free and it can’t hurt anything. A low score does not negate your SAT or ACT scores.
How do I begin using ALEKS?
Go to the ALEKS Assessment. You may need to install LockDown Browser. Before getting started, please review the ALEKS Respondus Student Startup Guide (PDF). (Note: Chromebooks are now compatible.)
Is there a fee for using ALEKS?
No, ALEKS is free. This includes everything.
Can I retake the ALEKS Placement Assessment?
Yes, you may take up to 5 placement assessments. However, to make each attempt worthwhile, it is important that you spend time working in your ALEKS Prep and Learning Module in between placement assessments so that you can improve your skills. Only the highest ALEKS score is used for placement.
Are ALEKS Placement Assessments proctored?
The placement assessments must be taken using LockDown Browser and Respondus Monitor (webcam).
May I use a calculator while using ALEKS?
ALEKS will provide an on-screen calculator if you need one to complete a particular problem. You may also use a single-line calculator. No graphing or two-line calculators can be used.
May I use any other resources during a placement assessment?
You may only use a pen or pencil, paper, and the resources provided by ALEKS. You may not receive assistance from friends, family, other websites, textbooks, or any other resource not provided by ALEKS. Using outside resources will lead to improper placement and ultimately course failure. Remember, your goal is to be successful in your first math course.
Can I retake the ALEKS Placement Assessment immediately?
You must wait 48 hours between placement assessments. There is generally no benefit to re-taking the assessment immediately after completing a prior attempt. Unlike the SAT or ACT, you cannot improve your results by simply re-taking the assessment without spending time in the Prep and Learning Module to refresh material that you may have forgotten or to learn new material.
Must I work in my ALEKS Prep and Learning Module between placement assessments?
- 2nd: Before taking your 2nd placement assessment, you must wait 48 hours.
- 3rd: Before taking your 3rd placement assessments, you must wait 48 hours and spend 3 hours in a Prep and Learning Module.
- 4th: Before taking your 4th placement assessment, you must wait 48 hours and spend an additional 3 hours in the Prep and Learning Module.
- 5th: Before taking your 5th and final placement assessment, you must wait 48 hours and spend an additional 3 hours in a Prep and Learning Module.
Are placement assessments timed?
Yes, you have 48 hours to complete a placement assessment once it has begun. You can take a break, however, if you wait more than 48 hours you have to start a new assessment and it will not count as one of your five attempts.
How long will a placement assessment take to complete?
Placement assessments require approximately 90 minutes to complete, but the amount of time will vary by student. We suggest you set aside two hours. There will be a maximum of 30 questions.
What is my placement result?
Your placement result is your percentage mastery on your best assessment. After completing each assessment, you will see this results page:
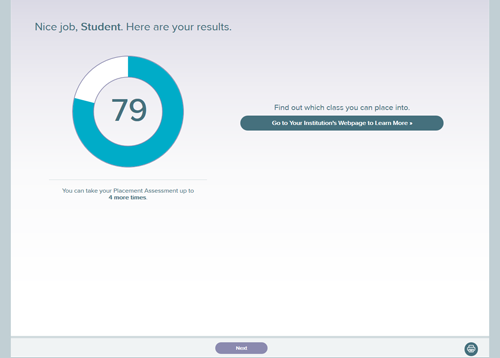
See the table of scores required for mathematics course placement or your advisor for more information about how Purdue uses your ALEKS scores.
Can I practice using ALEKS before I begin placement?
ALEKS will begin with a brief tutorial before your placement begins.
How long do I have access to my Prep and Learning Module?
You will have six months of access from the time that you start using your Prep and Learning module.
What are ALEKS Progress Assessments?
While working in a Prep and Learning Module, you will periodically complete progress assessments to solidify your gains in knowledge.
Does progress in an ALEKS Prep and Learning Module count toward placement?
No, you must complete a new placement assessment to change your placement result. Click on the placement tab on the upper right of the page from within ALEKS. Only your placement assessment results will be used for course placement.
Which Prep and Learning Module should I choose?
There are two to choose from. You should pick the one that matches the course description of the math course you are attempting to enroll. If you are not sure, pick Prep. for Calculus.
- PreCalculus: Trying to enroll in MA 13700 or MA 15300 or MA 15500 or MA 15800
- Preparation for Calculus: Trying to enroll in MA 16010, MA 16100, or MA 16500
Can I change to a different Prep and Learning Module later?
No, you may only use one Prep and Learning Module. Choose wisely.
What if I do not place into the course I wanted?
You can use a Prep and Learning Module to review and learn, and you may take another placement assessment to improve your placement result.
I did not place into the class I wanted. Can I take it anyway?
No, you must achieve the minimum placement result to take each corresponding class.
What if I placed into the class I wanted?
Congratulations! Continue to use your Prep and Learning Module to improve your chances of success. The placement result above is the minimum preparation required for your course! Take advantage of the targeted review and learning features in ALEKS to get a better grade in your class.
Where can I get help with ALEKS?
What about Advanced Placement (AP) credit?
You may still need to take ALEKS. However, all questions concerning advanced placement credit and the role of ALEKS in placement in non-mathematics courses should be directed to your advisor.
What is the deadline for taking ALEKS?
No deadline, however, you should complete it before meeting with your advisor to schedule your 1st semester classes.
Problems taking ALEKS?
If you are having problems with ALEKS, please contact ALEKS Technical Support:
Hours of Operation:
Sunday: 4:00 PM to 1:00 AM EST
Monday-Thursday: 7:00 AM to 1:00 AM EST
Friday: 7:00 AM to 9:00 PM EST
Phone: (800) 331-5094
Online: Submit a Support Request
Chat: Chat with a Representative