SymPy Worksheet

The Story So Far

You and your dog are walking along the beach at Lake Michigan on a hot day, playing fetch.

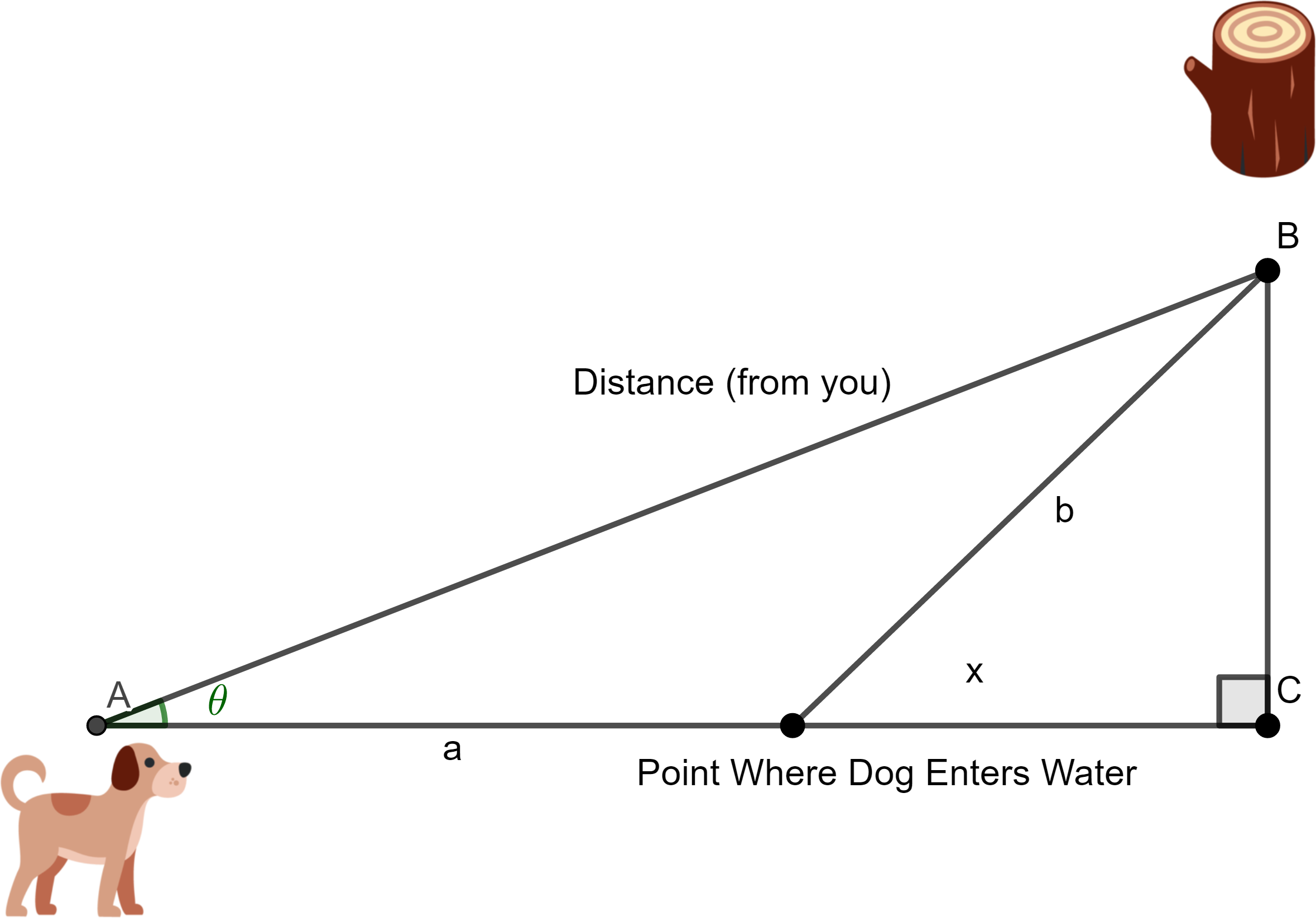
You throw the stick into the water ahead of you, $n$ meters from shore at the closest point.

Your dog can run about $S_{\text{run}}=8$ meters/second on land, and swim at about $S_{\text{swim}}=4$ meters/second. (you are very proud, he is a good boy.)

You are curious about whether your dog is a smart boy, so you want to calculate the optimum point where the dog enters the lake in order to fetch the stick.

Graded Assignment: In terms of the symbolic variables with $\LaTeX$ rendering:

Distance from shore $D_\text{you}$ - tell SymPy that this distance is positive.

The angle $\theta$ at which you throw the stick

use SymPy to solve for a single expression that gives the time until the dog reaches the stick. Pass it through sympy.simplify to get a (somewhat) canonized form. Render it as a $\LaTeX$ string and submit that string to Brightspace.

Let the distance be 10 meters and the angle be $\dfrac \pi 8$. Calculate the approximation, rounding to two decimal places.

Submit that answer to Brightspace.

For this exercise, you may assume that the angle is shallow enough that the dog will both run along the shore and swim, at least a little.

Make sure to keep track of your units (for your own sake) when constructing the expressions. If you are getting unreasonable answers - or no answers - that might be why!

It also helps to make sure your time makes sense. It'll take the dog a positive number of seconds - $t>0$ - and swimming directly is easy to calculate, so the minimum time $t$ satisfies $ 0 < t \leq \dfrac {10}4 $.

If you are a bit rusty on these related rates problems - remember right triangles are your friends, and to try to define a single new variable to optimize off of.

(in this case, the length the dog does not run along the beach $ x:= \cos(\theta) \cdot D_{\text{you}}-a$ is a good choice for that variable.)

Solving with Conditions, More Symbols

As a bonus challenge, solve in general terms for all dogs:

$S_{\text{run}}$ your dog's land-speed in meters/second
$S_{\text{swim}}$ your dog's lake-speed in meters/second

You can use sympy.piecewise to create an expression which correctly evaluates the time for any positive distance and reasonable angle between 0 and 90.

(This story actually happened to a professor up in Michigan, whose dog was a very smart boy.)