Definition 62.
autonomous
\begin{equation*}
\frac{dy}{dx}=f(y)\text{.}
\end{equation*}
Print preview
Handout Lesson 10, Equilibrium Solutions and Stability
Textbook Section(s).
This lesson is based on Section 2.2 of your textbook by Edwards, Penney, and Calvis.
CITATION: This set of notes contains several slope fields and solution curves sketched in the slope fields. I used the direction field plotter by Ariel Barton at the Unviersity of Arkansas to create these pictures.
Autonomous Differential Equations, Critical Points, and Equilibrium Solutions.
With the logistic model \(\frac{dP}{dt}=kP(M-P)$\) \(P \equiv \fillinmath{XXXXXXXXXXXXXXX}\) and \(P \equiv \fillinmath{XXXXXXXXXXXXXXX}\) are constant solutions. These constant solutions separate the other solutions into three categories, depending on the value of \(P_0\text{.}\)
Let’s consider the logistic growth model
\begin{equation*}
\frac{dP}{dt}=P(2-P)
\end{equation*}
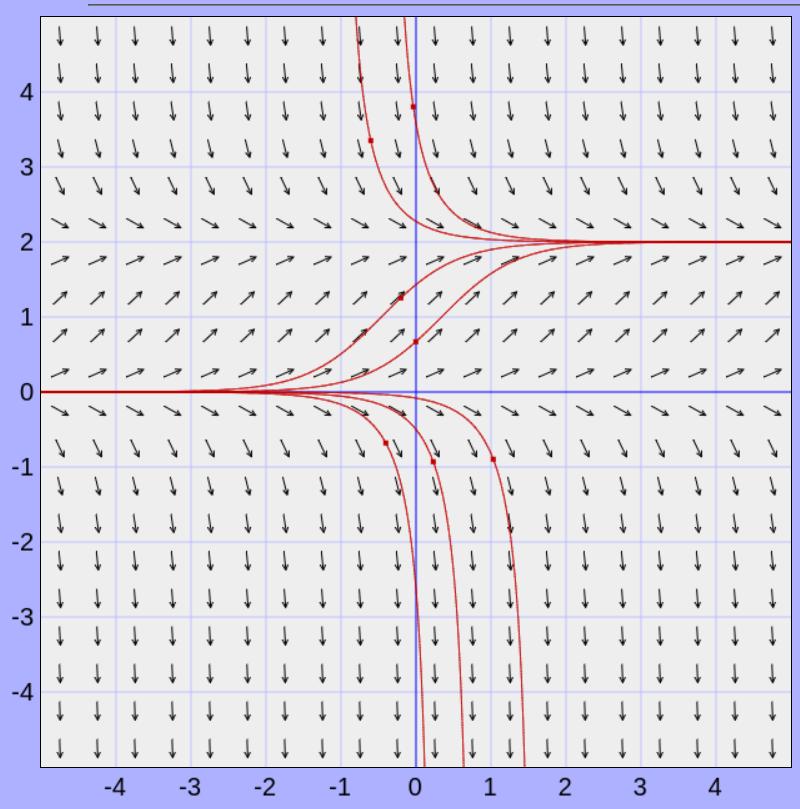
The following slope field and solution curves were generated by the direction field plotter by Ariel Barton.
A slope field for \(\frac{dP}{dt}=P(2-P)\text{.}\)
Definition 64.
The solutions of \(f(y)=0\) are the critical points of the autonomous differential equation
\begin{gather}
\frac{dy}{dx}=f(y)\tag{✶✶}
\end{gather}
Phase Diagrams and Stability.
Let’s take another look at the slope field diagram that we saw earlier for the logistic model \(\frac{dP}{dt}=P(2-P)\text{.}\)
As \(t \rightarrow \infty\text{:}\)
-
the diagram around \(P \equiv 0\) looks like a “”. We call \(P= 0\) an critical point of the model.
-
the diagram around $P \equiv M$ looks like a “”. We call \(P= 0\) an critical point of the model.
We do not need to see the slope field to understand the stability of a critical point. We can analyze the derivative algebraically.
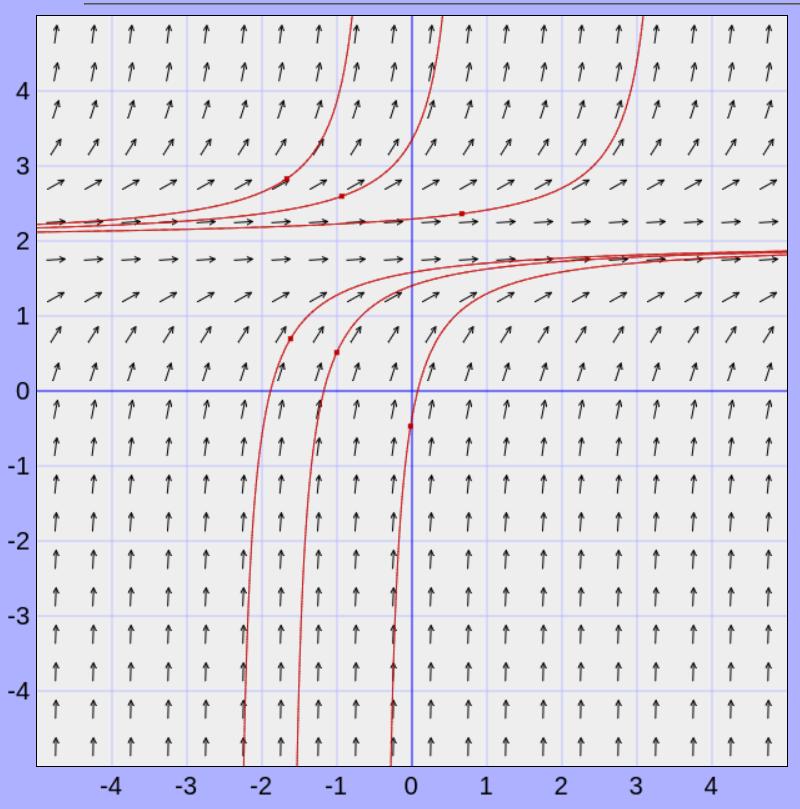
Example 66.
Discuss the stability of the critical point(s) of the model. \(\frac{dx}{dt}=(x-3)^2\text{.}\)
A slope field for \(\frac{dx}{dt}=(x-3)^2\text{.}\)
The Effect of Parameters - Bifurcation.
Parameters can have a significant effect on the type of solutions you obtain for a differential equation. For example, parameters can affect critical points.
Example 67. Bifurcation point.
(Based on Number 21 from Section 2.2 of your textbook by Edwards, et.al.)
Consider the model
\begin{gather}
\frac{dx}{dt}=kx-x^3=-x(x^2-k)\tag{†}
\end{gather}
with parameter \(k\text{.}\)
We can visualize this by plotting all points
\begin{equation*}
(k,c)
\end{equation*}
A Cartesian coordinate system with independent variable \(k\) and dependent variable \(c\text{.}\)
Harvesting Logistic Populations.
Consider the logistic model that has been slightly modified to account for harvesting of a population (such as fishing or butchering beef).
\begin{align*}
\frac{dP}{dt} & = kP(M-P)-h \\
& = -kP^2+kMP-h
\end{align*}
where \(k, M, h>0\) and \(h\) represents the rate at which the population is being harvested.
-
The quadratic equation has 2 distinct real roots \(H\) and \(N\) with \(H<N\text{.}\) Using the quadratic formula, it can be argued that \(0 < H < N < M\text{.}\) (See example 4 in section 2.2 of your textbook by Edwards, et.al.)
-
There is one distinct real root \(N\text{.}\)
-
There are no real roots.\begin{equation*} \frac{dP}{dt}= -kP^2+kMP-h \end{equation*}
Let’s consider the harvesting model
\begin{equation*}
\frac{dP}{dt}=P(6-P)-h = -P^2+6P-h
\end{equation*}
where \(k=1\) and \(M=6\text{.}\) Let’s look at what happens for some values of \(h\text{.}\) The direction fields on this page were made Ariel Barton’s direction field plotter. The graphs of parabolas were created using Desmos.
- \(h=0\) (This is just a logistic growth model)
- \(h=4\)
- \(h=9\)
- \(h=10\)
