Use a linear approximation to estimate \(\sqrt{4.1}\text{.}\)
The graph of \(y=f(x)=\sqrt{x}\) and its tangent line at \((4,2)\text{.}\)
Print preview
Handout Lesson 12, Euler’s Method, A Numerical Method for Solving IVP’s
Textbook Section(s).
This lesson is based on Sections 2.4 and 2.5 of your textbook by Edwards, Penney, and Calvis.
Motivation.
Let’s take a step back in time to your Calculus I class. One of the concepts that you are supposed to glean from your Calculus I class is that if the function \(f\) is differentiable at \(x_0\) and \(L(x)\) is the equation for the tangent line to \(f\) at \(x_0\text{,}\) then
\begin{equation*}
f(x_1) \approx L(x_1)
\end{equation*}
if \(x_1\) is sufficiently close to \(x_0\text{.}\) This is the idea behind linear approximations. (This is also the first step in using Taylor polynomials to approximate function values.)
Example 70.
Euler’s Method.
Euler’s Method is used to approximate points on the solution curve of an IVP.
\begin{gather}
\frac{dy}{dx}=f(x,y), \qquad y(x_0)=y_0\tag{✶}
\end{gather}
We are interested in the function
\begin{equation*}
y(x)
\end{equation*}
which is a solution of (✶). Unlike linear approximation problems, we do not have the function (unless it is a really special differential equation that is easy to solve). We only have its derivative. Because the IVP provides us with the point \((x_0,y_0)\text{,}\) the derivative is all we need to find an equation for the tangent line to the solution curve through this point. We will then use that tangent line to approximate the \(y\)-value of the point on the solution curve at \(x=x_1=x_0+h\text{,}\) for some small \(h\) value. This new point, \((x_1,y_1)\) probably is not on the solution curve, \(y=y(x)\text{,}\) but we hope that it is close to the solution curve. So we pretend that it is on the solution curve, use the derivative we are given in the IVP to construct a "tangent line" to \(y=y(x)\) "at" \((x_1,y_1)\text{,}\) and use this "tangent line" to approximate the \(y\)-value of the point on the solution curve at \(x=x_2=x+2h\text{.}\) The process continues until you reach a desired stopping point.
The picture below is Figure 2.4.1 of your textbook by Edwards, et.al.
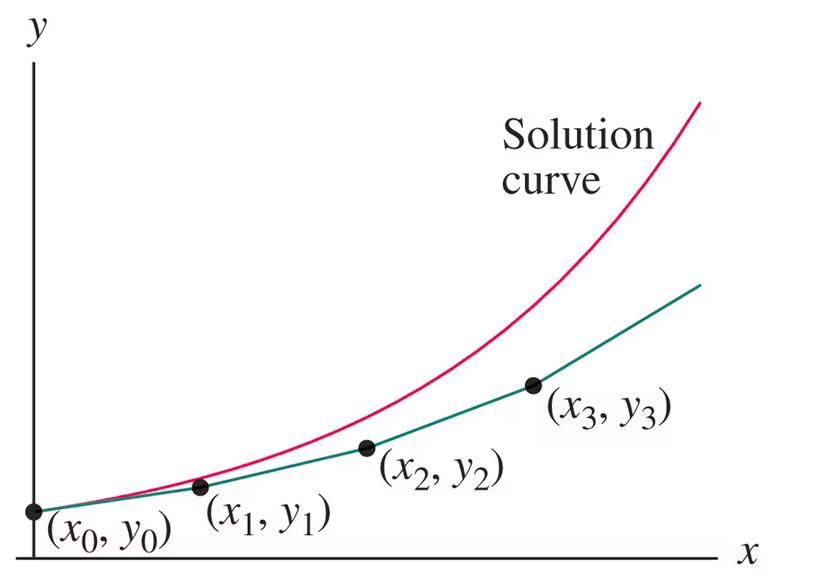
A picture of the solution curve for an IVP and the Euler approximation curve. The Euler approximation curve is a piecewise linear curve connecting the Euler approximation points. In this example, only \((x_0, y_0)\) is on the solution curve. There are errors in the other approximation points.
Algorithm 71. Euler’s Method for Approximating Solutions for IVP’s.
Given:
-
An IVP\begin{equation*} \frac{dy}{dx}=f(x,y), \qquad y(x_0)=y_0 \end{equation*}
-
A step size \(h \neq 0\)
Return: A list \([y_0, y_1, y_2, y_3, \dots, ]\) where
\begin{align*}
x_n & = x_0+nh \\
y_{n+1} & = y_n+hf(x_n,y_n)
\end{align*}
for \(n \in \set{1, 2, 3, \dots}\text{.}\)
Comments
-
Unless you only need to do three or fewer steps, computers should be used.
-
On the exam, it is very possible (I have seen it before) that you will be required to do a few steps. So make sure that you do not become so computer dependent on these problems that you cannot perform 3 steps of this algorithm by hand.
Example 72. Using Euler’s method.
(Based on Number 7 from Section 2.4 of your textbook by Edwards, et.al.)
Use Euler’s method with step size 0.2 to find \(y_1\) and \(y_2\) for the IVP.
\begin{equation*}
\frac{dy}{dx}=-3x^2y, \qquad y(0)=3
\end{equation*}
Let’s use MATLAB to verify our results. The department has provided a MATLAB file eul.m that you may use. It is on the course website. I have also posted it in the Extra Resources module for our course in Brightspace.
To begin, I created a text file for my function named fcn1.m. The contents of that file are shown below.
function W=fcn1(x,y)
W=-3*x^2*y;
In a terminal, I navigated to the directory that contained eul.m and fcn1.m. I then ran the following commands:
>> [x,y]=eul('fcn1',[0,0.4],3,0.2);
>> [x,y]
which produced
ans =
0 3.0000
0.2000 3.0000
0.4000 2.9280
The following pictures were based on a YouTube video by Ajit Kumar I used SageMath to create the pictures.
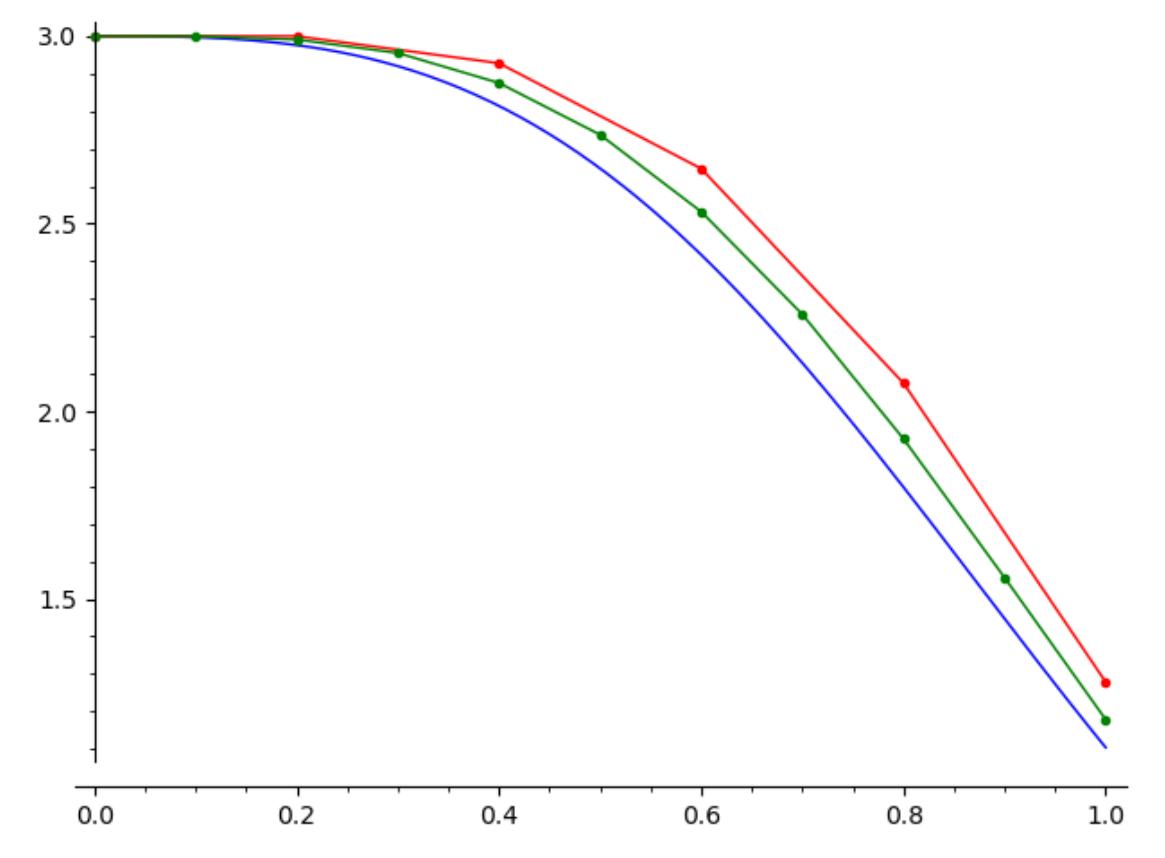
For the IVP
\begin{equation*}
\frac{dy}{dx}=-3x^2y, \qquad y(0)=3\text{,}
\end{equation*}
I have graphed the solution curve \(y(x)=e^{-x^3}\text{,}\) the Euler approximation curve on \([0,1]\) using \(h=0.2\text{,}\) and the Euler approximation curve using \(h=0.1\text{.}\)
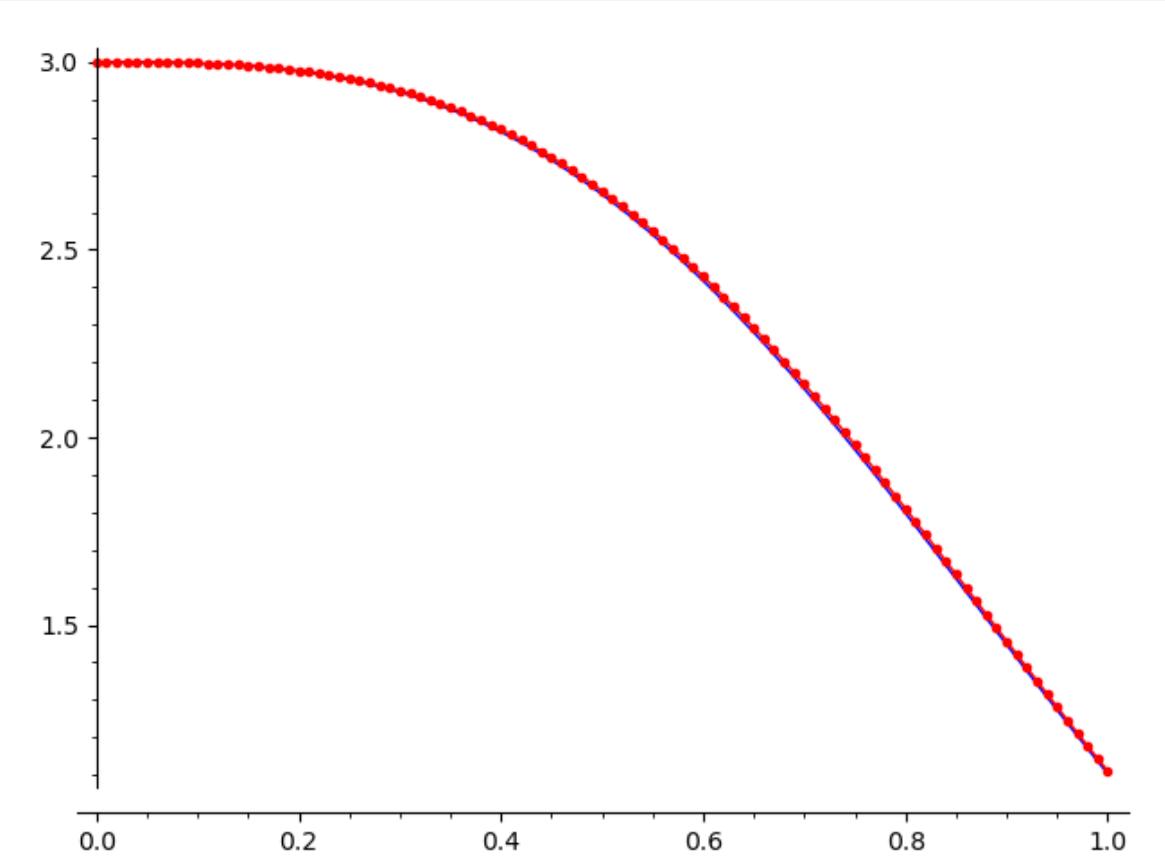
In the next picture, I have graphed the solution curve \(y(x)=e^{-x^3}\) and the Euler approximation curve on \([0,1]\) using \(h=0.01\text{.}\)
Improved Euler Method.
The picture below is Figure 2.5.3 in your textbook by Edwards, et.al. It is used to explain the Improved Euler Method Algorithm for approximating points on the solution curve of an IVP.
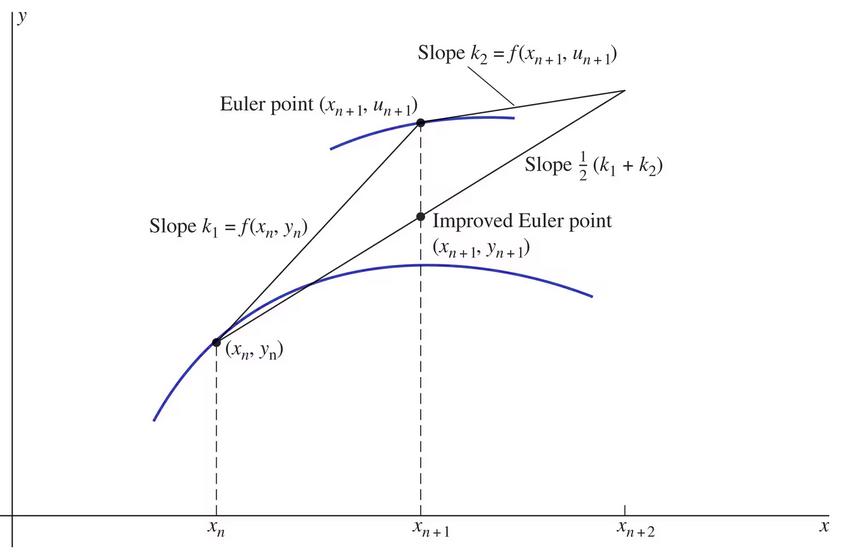
The starting point, the Euler point, and the improved Euler point
Algorithm 73. Improved Euler Method for Approximating Solutions for IVP’s.
Given:
-
An IVP\begin{equation*} \frac{dy}{dx}=f(x,y), \qquad y(x_0)=y_0 \end{equation*}
-
A step size \(h \neq 0\)
Return: A list \([y_0, y_1, y_2, y_3, \dots, ]\) using the following algorithm:
-
\(x_n = x_0+nh\text{,}\) \(x_{n+1}=x_0+(n+1)h\)
-
\(\displaystyle k_1=f(x_n,y_n)\)
-
\(\displaystyle u_{n+1}=y_n+hk_1\)
-
\(\displaystyle k_2=f(x_{n+1},u_{n+1})\)
-
\(\displaystyle y_{n+1} = y_n+h\frac{1}{2}(k_1+k_2)\)
for \(n \in \set{1, 2, 3, \dots}\text{.}\)
Example 74. Comparing Euler’s Method and the Improved Euler Method.
(Based on Number 4 from Section 2.5 of your textbook by Edwards, et.al.)
-
Use the improved Euler method to approximate the solution of the IVP on \([0,1]\) with step size \(h=0.1\text{.}\)NOTE: The improved Euler method is implemented in the MATLAB file rk2.m, which is available from the Course Web Page or from the Extra Resources module in our Brightspace page. It is implemented in exactly the same way that eul.m is implemented.Here are the results from MATLAB:
ans = 0 1.0000 0.1000 0.9100 0.2000 0.8381 0.3000 0.7824 0.4000 0.7416 0.5000 0.7142 0.6000 0.6988 0.7000 0.6944 0.8000 0.7000 0.9000 0.7145 1.0000 0.7371 -
It can be shown that the solution curve is \(y=2e^{-x}+x-1\text{.}\) Let’s compare the approximate function values and the function values.
\(x_i\) Euler \(y_i\) Improved Euler \(y_i\) \(y(x_i)\) 0.0000 1.0000 1.0000 1.0000 0.1000 0.9000 0.9100 0.9097 0.2000 0.8200 0.8381 0.8375 0.3000 0.7580 0.7824 0.7816 0.4000 0.7122 0.7416 0.7406 0.5000 0.6810 0.7142 0.7131 0.6000 0.6629 0.6988 0.6976 0.7000 0.6566 0.6944 0.6932 0.8000 0.6609 0.7000 0.6987 0.9000 0.6748 0.7145 0.7131 1.0000 0.6974 0.7371 0.7358
The following picture was based on a YouTube video by Ajit Kumar. I used SageMath to create the pictures.
For the IVP
\begin{equation*}
\frac{dy}{dx}=x-y, \qquad y(0)=1\text{,}
\end{equation*}
I have graphed the solution curve \(y(x)=2e^{-x}+x-1\text{,}\) the Euler approximation curve, and the improved Euler approximation curve both on \([0,1]\) and using \(h=0.1\text{.}\)
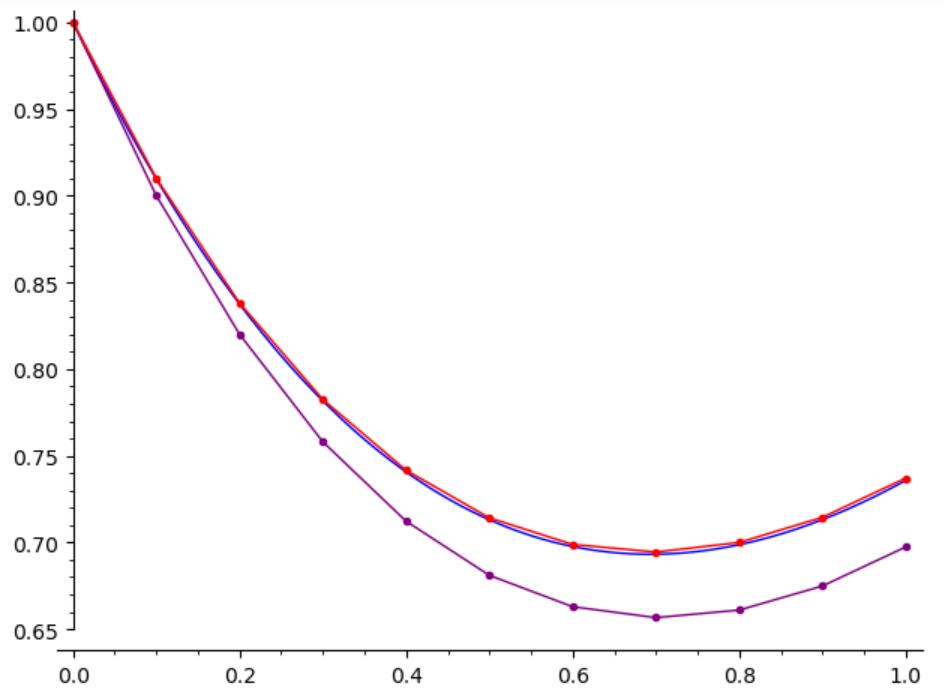
The error is evident between the solution curve and the Euler approximation. The error between the solution curve and the improved Euler approximation is almost indistinguishable.
