Print preview
Handout Lesson 17, Mechanical Vibrations
Textbook Section(s).
This lesson is based on Section 3.4 of your textbook by Edwards, Penney, and Calvis.
Trigonometry.
It is easy enough to look up the difference formulas for the sin and cosine functions.
\begin{align*}
\cos(\alpha-\beta) &
=\cos(\alpha)\cos(\beta)+\sin(\alpha)\sin(\beta)\\
\sin(\alpha-\beta) & =\sin(\alpha)\cos(\beta)-\cos(\alpha)\sin(\beta)
\end{align*}
I am not going to spend time on this in class today, but if you are interested, you can actually see this formula and the addition formula for the sine function from Euler’s identity.
\begin{align*}
\cos(\alpha-\beta)+i\sin(\alpha-\beta) & =
e^{i(\alpha-\beta)} \\
& =
e^{i\alpha}e^{i(-\beta)} \\
& =
\left(\cos(\alpha)+i\sin(\alpha)\right)\left(\cos(-\beta)+i\sin(-\beta)\right)\\
& =
\left(\cos(\alpha)+i\sin(\alpha)\right)\left(\cos(\beta)-i\sin(\beta)\right)\\
& =
[\cos(\alpha)\cos(\beta)+\sin(\alpha)\sin(\beta)]\\
&
\qquad + i[\sin(\alpha)\cos(\beta)-\cos(\alpha)\sin(\beta)]
\end{align*}
We are going to use the difference identity for cosine many times today to convert a function of the form \(A\cos(\mu t) + B\sin(\mu t)\) into a function of the form \(K\cos(\omega t-\gamma)\text{.}\)
Example 124. Converting to \(f(t)=K\cos(\omega t-\gamma)\) form.
Springs.
The following diagram for a spring with a dashpot was taken from section 3.4 of your textbook.
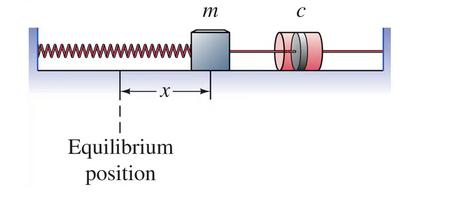
A mass-spring-dashpot system
Potentially, there are three different forces controlling the position, \(x(t)\) of this mass:
-
\(F_s=-kx\text{,}\) the force from the spring to restore the system to equilibrium (\(x=0\) when the spring is not stretched or compressed.)
-
\(F_R=-cv=-cx'\text{,}\) the force from the dashpot, damper, shock absorber, or friction
-
\(F_E\text{,}\) an external force
Newton’s law gives us:
\begin{equation*}
ma = F_s +F_R +F_E
\end{equation*}
which implies
\begin{equation*}
mx''+cx'+kx=F_E
\end{equation*}
Vocabulary for springs.
For the spring equation
\begin{equation*}
mx''+cx'+kx=F_E
\end{equation*}
-
spring constant
-
damping constant
-
undamped motion
-
damped motion
-
free motion
-
forced motion
A comment on the spring constant and units.
When you are working with springs, all of the units will cancel correctly if
-
the mass is in kg
-
the force applied to stretch the spring is in N
-
the distance that the spring is stretched is in m
Free undamped motion.
\begin{equation*}
mx''+kx=0
\end{equation*}
Example 126. An undamped system.
A mass of 2 kg is attached to a spring with spring constant 50 N/m. There is no damping. Find a formula for \(x(t)\text{,}\) the position function, if \(x_0=5\) and \(v_0=-10\text{.}\) Then identify the amplitude, circular frequency, period, frequency, and time lag of the system.
Free damped motion.
\begin{equation*}
mx''+cx'+kx=0
\end{equation*}
If the characteristic equation has:
-
2 real roots, the system is overdamped
-
1 real root, the system is critically damped
-
2 complex roots, the system is underdamped
For initial conditions: \(x_0=5\) an \(v_0=-10\text{,}\) we would have the following differential equation/solution pairs.
| Differential Equation | Solution | Type |
|---|---|---|
| \(2x''+50x=0\) | \(x(t)=\sqrt{29}\cos(5t-5.90268)\) | undamped |
| \(2x''+12x'+50x=0\) | \(x(t)=\frac{5\sqrt{17}e^{-3t}}{4}\cos(4t-0.24498)\) | underdamped |
| \(2x''+20x'+50x=0\) | \(x(t)=5e^{-5t}+15te^{-5t}\) | critically damped |
| \(2x''+52x'+50x=0\) | \(x(t)=\frac{115}{24}e^{-t}+\frac{5}{24} e^{-25t}\) | overdamped |
I used Desmos to graph our solutions:
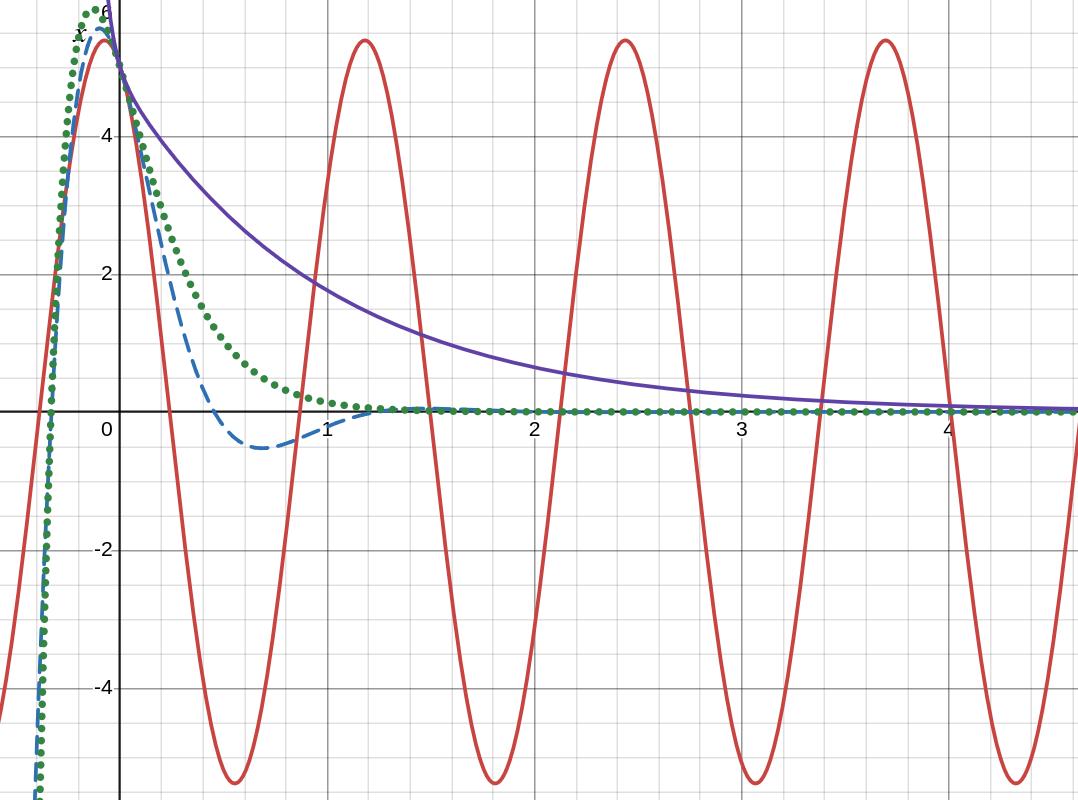
Graphs of four systems: an undamped system, an underdamped system, a critically damped system, and an overdamped system.
